
行测数量关系题答题技巧
行测排列组合之巧解“隔板模型”问题
排列组合作为行测试卷中考察概率较大但略有难度的考点,一直为考生所头疼。因此为了熟悉这一问题,了解并掌握排列组合中常见的几种题型的解题技巧便显得尤为重要。而“隔板模型”就是其中较为典型的一种题型。接下来就带大家学习一种巧解方法“隔板法”来解决此类问题。
“隔板模型”题型特点很具有辨识性:n个相同元素分给m个不同对象,每个对象至少分得1个元素。则一共有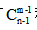 种分法。
种分法。
例1
10个相同的苹果分给3个小孩,每个小孩至少分得1个苹果,有多少种分法?( )
A.30B.36C.45D.55
【答案】B【解析】由题目可知,10个相同的苹果分给3个不同的小孩,每个小孩至少分得一个,可以理解为将这10个苹果分成3堆,每堆苹果给对应的小孩即可。如何快速分堆呢?我们不妨把这10个苹果从左至右依次排成一排,如果要求分成两堆,则只需要在相邻苹果之间的空隙中放置一个隔板,便分成了左右两堆。同理要求分成3堆,则需要在苹果之间找2个不同的空隙放置2个隔板,如右示意图所示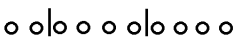 。而10个苹果之间有9个不同的空隙,那么我们就要在这9个不同空隙中任意选取2个空隙放置隔板即可,
。而10个苹果之间有9个不同的空隙,那么我们就要在这9个不同空隙中任意选取2个空隙放置隔板即可,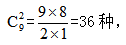 本题选择B项。
本题选择B项。
例2
12台相同电脑分配给3个不同的办公室,每个办公室至少分得3台电脑,有多少种分法?( )
A.8B.10C.12D.14
【答案】B【解析】由题目可知,这道题在分配方式上发生了变化,不再是每个对象至少分1个,所以不能直接由结论列式求解。此时我们就需要将题干中不满足隔板模型基本特征的条件进行转化。由于每个办公室至少分得3台电脑,不妨先给每个办公室先各分2台,此时还剩下12-3×2=6台。此时题干就变为了将剩下的6台相同电脑分给3个不同办公室,每个办公室至少分得1个。满足“隔板模型”题型特点,所以一共有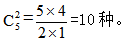 本题选择B项。
本题选择B项。
例3
将12个一样的汽车模型全部分给3个小朋友,任意分,共有多少种不同的分配方式?( )
A.91B.100C.121D.135
【答案】A【解析】由题目可知,这道题不满足每个对象至少分1个的特征,所以同样需要进行转化。任意分即说明有的小朋友可以不分得汽车模型,换言之可以理解为每个小朋友至少分得0个。那不妨先从每个小朋友手上借来1个,则共借来3个,加上原有的12个,共有15个汽车模型。由于最初向每人借了一个,此时再去分配肯定是要还的,所以这15个模型每人至少分得1个,满足隔板模型基本特征,直接利用结论,共有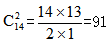 种分配方式。本题选择A项。
种分配方式。本题选择A项。
相信大家通过上述三道题目,对于隔板模型的基本题型特征和变式类型有了更进一步的了解。需要注意的是,在面对变形题目时,需运用先分或先借的思想将题干转化成标准模型去求解。希望对于本次“巧解”隔板模型的方法讲解对大家有所帮助。
行测点睛:如何快速识别用“A”还是用“C”
针对排列组合这个题型,很多学生之所以觉得排列组合比较难?非常重要的原因就是“A”和“C”傻傻的分不清。所以今天就来谈一谈如何快速识别用“A”还是用“C”。
我们先来看一下什么是排列、组合。排列指的是从n个不同的元素中任取m个按照一定的顺序排成一列,排列种数记作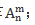 组合指的是从n个不同的元素中取出m个元素作为一组,组合种数记作
组合指的是从n个不同的元素中取出m个元素作为一组,组合种数记作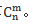 通过上面的描述我们会发现排列与组合区别在于是否有顺序要求,有顺序要求是排列,没有顺序要求是组合。这个时候肯定会有同学说道理我们都懂,但是在实际做题的时候就是因为分不清题目到底要不要考虑顺序。这个正是我们要说的核心的问题,在实际考试中我们可以通过交换元素顺序观察对结果有无影响,有影响用排列数A,无影响用组合数C。下面我们一起来看几道题目来巩固一下。
通过上面的描述我们会发现排列与组合区别在于是否有顺序要求,有顺序要求是排列,没有顺序要求是组合。这个时候肯定会有同学说道理我们都懂,但是在实际做题的时候就是因为分不清题目到底要不要考虑顺序。这个正是我们要说的核心的问题,在实际考试中我们可以通过交换元素顺序观察对结果有无影响,有影响用排列数A,无影响用组合数C。下面我们一起来看几道题目来巩固一下。
例1
某集团公司组建新的子公司,有8人竞聘子公司的总经理,财务总监、行政总监、销售总监和技术总监五种职务,最后每种职务都有一个人担当且每个人只能担当一种职务,则共有结果多少种?( )
A.6720B.840C.40320D.120
【答案】A【解析】题目要求我们从8个人里面选择5个人分别担任五种职务,属于排列、组合问题。这就需要我们判断是用排列数计算,还是组合数计算。可以通过交换元素顺序对结果有无影响判断,假设选取的五个人中有两个人是甲和乙,不妨认为甲是总经理,乙是财务总监;交换甲和乙的顺序,变成甲是财务总监,乙是总经理。很明显,这是两种不同结果,说明交换元素顺序对结果产生影响。所以用排列数计算,共有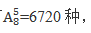 故选择A。
故选择A。
例2
某大学考场在8个时间段内共安排了10场考试,除了中间某个时间段(非头尾时间段)不安排考试外,其他每个时间段安排1场或2场考试。那么,该考场有多少种考试安排方式(不考虑考试科目的不同)?( )
A.210B.270C.280D.300
【答案】A【解析】先从中间6个时间段中选择一个不安排考试。有6种。接下来给剩余7个时间段各安排一场考试。然后再从这7个时间段中选择3个各安排一场考试。从7个里面选择3个属于排列、组合问题,利用交换元素顺序对结果有无影响进行判断。由于题目要求不考虑考试科目的不同,所以交换顺序对结果不会产生影响,应该用组合数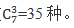 所求为6×35=210,故选择A。
所求为6×35=210,故选择A。
综上所述,快速区分用“A”还是用“C”核心关键就是交换一下元素的顺序观察对结果有无影响,有影响用排列数A,无影响用组合数C。
行测数量关系:多者合作到底谁在“加班”
行测考试成了各位同学成功的“拦路虎”,而在行测中数量关系常常是同学们比较痛苦的一个版块,尤其是其中的工程问题。工程问题分为普通工程问题和多者合作工程问题,解题原则是通过核心公式掌握各种考题,部分题型会通过设特值的实用方法来解题。接下来给大家介绍一下多者合作的题型和解题技巧。
基本公式
工作总量=工作效率×工作时间,通常用字母表示为W=p×t
基本概念
多者合作:工程问题当中,多个人共同去完成一项工作。(多者合作总效率等于各部分效率之和)
应用环境及方法
例1
某项工程,甲施工队单独干需要30天才能完成,乙施工队需要40天才能完成,甲、乙合作干了10天,因故停工10天,再开工时甲、乙、丙三个施工队一起工作,在干4天就可全部完工。那么丙队单独干需要大约( )天才能完成这项工程。
A.21B.22C.23D.24
【答案】B【解析】设工作总量为30和40的最小公倍数120,则甲的工作效率为4,乙的工作效率为3。甲、乙合作10天的工作量为(3+4)×10=70,则剩余120-70=50个工作量,甲、乙、丙三个施工队一起工作4天完成,则三人效率和为50÷4=12.5,丙的工作效率为12.5-4-3=5.5,丙单独完成这项工程所需要时间为120÷5.5=21.8天,选项均为整数天,故选择22天,本题选择B项。
例2
甲、乙、丙三人共同完成一项工程,他们的工作效率之比是5∶4∶6。先有甲乙合作6天,再由乙单独做9天,完成全部工作的60%。若剩下的工程由丙单独完成,则丙所需要的天数是:( )
A.9B.11C.10D.15
【答案】C【解析】设甲效率为5,乙效率为4,丙效率为6。甲乙合作6天工作量为(5+4)×6=54,乙单独工作9天工作为4×9=36,此时两人完成工作之和54+36=90占全部工作量60%,可得工程工作总量为90÷60%=150,则剩余工作量为150×(1-60%)=60,丙单独完成剩余工作量所需时间为60÷6=10天,故本题选择C项。
总结
1.当题干中给出若干单独完工的时间,可以将时间的最小公倍数特值为工作总量,进而求出工作效率。
2.当题干给出或可以推出效率之比,将效率的最简比数值特值为对应效率,进而求出工作总量。
备考行测数量关系最重要的是多练习、多概括、多总结,才能突破自我完成逆袭,希望以上的总结能够帮助同学们更好的掌握相关题型。
行测数量关系:三步让你明白和定最值问题
对于数量关系这一部分,有一类相对比较简单的题目,叫做和定最值题目。
和定最值问题顾名思义,就是几个量的和一定时,求某个量的最大值最小值。
对于和定最值问题,它的解题原则就是:求某个量的最大值,那么其他的量就要尽可能小;相反,若求某个量的最小值,那么其他的量就要尽可能大。而我们在解题时,往往结合方程法去进行求解,会更清楚更快速一点,通常求谁就设谁为未知数。
而这就是解决和定最值的三步走,第一步设未知数,第二步表示出其他量,第三步列等式。
举个例子:5个已经成年的男生,他们的年龄不等且年龄之和是120岁,那么这五个男生中,年龄最大的男生最大是几岁?
那么在这里,已经告诉我们,5个人的年龄和为120,也就是和一定,现在求的是年龄最大的人的最大值,那这就是非常典型的一个和定最值问题。
如下表:五人年龄依次按照从大到小排列。首先第一步,设年龄最大的人为x岁;第二步,求最大其他量尽可能小,那么先确定最小的量,最小的人又要满足已成年,故最小的人18岁,第四大的人要尽可能小又要比最小的大,故第四大的人最小为19岁,以此类推第三大的人为20岁,第二大的最小为21岁;第三步,根据年龄之和为120可得:x+21+20+19+18=120。解得x=42。

所以数量关系是不是也没有大家所想的都那么困难呢,也是有一些题型是我们可以去“挣扎”一下的,那么后续如果同学们在做题时如果遇到这类的题型,就可以用这三步走去进行求解了。那么我们一起来做一道例题来检验一下大家的成果吧。
例题
一个工序由5个工人负责,平均每人一个小时完成12个零件,已知每名工人的工作效率互不相同,且最慢的工人一小时可以完成3个零件,求效率最快的工人最多完成了多少个零件?( )
A.42B.43C.41D.40
【解析】
如下表:五人的工作效率按照从大到小依次排列,题中已知5个人平均效率,由此可得5人在一小时内所做的总零件数,也就是5×12=60个,也就是5个人一个小时的效率总和一定,又告知效率各不相等,求最大量的最大值,那么就设最快的人每小时完成x个,紧接着让其他量尽可能小,先确定最小,也就是最慢的工人,题中已经告知为3个,第四大要尽量小且比最慢的大,故为4个,第三大为5,第二大为6,根据题意列出等式:x+6+5+4+3=60,解得x=42,故选A。

相信在同学们的不懈努力练习之下,一定可以熟练掌握此类题目。
行测趣味题:草逃,牛追,他们都插翅难飞
在数量关系中,行程问题分成了很多种题型,今天带领大家学习其中较为简单的题型——牛吃草问题。牛吃草问题的题干描述一般会出现类似于排比句的句式并且原始固定量受到两个主体的影响。
牛吃草的基本题型包含以下三类:
追及型牛吃草问题
特征:牧场上有一片匀速生长的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身生长使草量增加。(注:牛吃草的速度大于草自身生长的速度)。
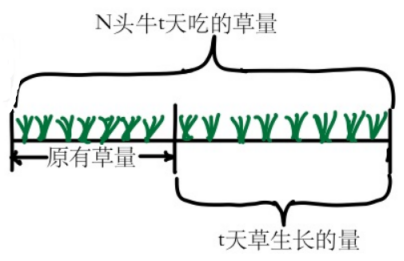
假设每头牛每天吃1份草,这片草场草每天的生长速度为x份,t天牛把草吃完。则:原有草量=(牛每天吃掉的量-草每天生长的量)×天数=(N-x)×t。
相遇型牛吃草问题
特征:牧场上有一片匀速枯萎的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身枯萎也使草量减少。
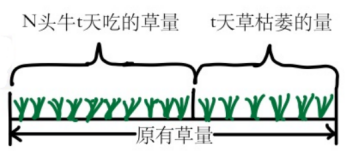
假设每头牛每天吃1份草,这片草场草每天的枯萎速度为x份,t天牛把草吃完。则:原有草量=(牛每天吃掉的量+草每天枯萎的量)×天数=(N+x)×t。
极值型牛吃草问题
特征:发生在追及型牛吃草问题中,但问法一般为“为了保持草永远吃不完,那么最多能放多少头牛吃”。
当牛吃草的速度>草生长速度,草一定能吃完。当牛吃草速度≤草生长速度,草永远吃不完,而现在问最多放多少头牛,故取等号。即当牛的数量N=草生长速度x时,草永远吃不完。
综上所述,大家在解决牛吃草问题时,关键在于:
1、判定追及还是相遇:找出影响原始固定量的两个因素,影响相反(一增一减)为追及,影响相同(两减)为相遇。
2、运用对应牛吃草公式,一般以原有草量不变建立等量关系。
但在考试中,牛吃草问题经常结合超市收银台结账、漏船排水、窗口售票、泄洪、伐木等各种背景出现,所以各位同学需通过“问题以类似排比句句式描述”这一明显特征识别牛吃草问题,再判定具体的考察题型,运用公式解题。
通过以上介绍,相信各位同学已经了掌握牛吃草问题的解题思路,希望各位同学多加练习,未来在考试中取得好成绩。
行测数量关系:小小的篱笆 大大的菜园
大家以前可能接触过均值不等式的题目:如何用固定长度的篱笆围成一个面积最大的菜园?这个题目它无非就是研究和与积之间的关系!所运用的知识点是基于均值不等式的两个结论,我们一起来学习!
什么是均值不等式
若a、b为实数,则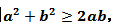 当且仅当a=b时,“=”号成立。
当且仅当a=b时,“=”号成立。
均值不等式的结论
1、若a+b为定值,a、b间的差值越小,a、b乘积越大,当且仅当a=b时,ab取得最大值。
2、若ab为定值,a、b间的差值越小,a、b和越小,当且仅当a=b时,a+b取得最小值。
简记为,和定差小积大,积定差小和小。
经典例题
例1
某农户要用篱笆将自己的菜园围起来,已知篱笆的总长度为48米。请问农户的菜园面积最大为多少平方米?( )
A.100B.120C.144D.156
【答案】C【解析】设篱笆的长宽分别为a,b,则2×(a+b)=48,可得a+b=24。求菜园的面积最大为多少平方米,即求ab的最大值。根据均值不等式的结论:当a=b=12时,ab取得最大值为12×12=144。故菜园的最大面积为144平方米,正确答案为C。
例2
建造一个容积为16立方米,深为4米的长方体无盖水池,如果池底和池壁的造价分别为每平方米160元和每平方米100元,那么该水池的最低造价是多少元?( )
A.3980B.3560C.3270D.3840
【答案】D【解析】若假设长方体无盖水池底的边长分别为a、b,则池底的面积为a×b=16÷4=4平方米,则可得水池的最低造价为4×160+(a×4×2+b×4×2)×100=640+800×(a+b),求最低造价,即求a+b的最小值,符合乘积一定,求和最小,当且仅当a=b=2时,a+b的和最小为4,则最低造价为640+800×(a+b)=640+800×(2+2)=3840,故选择D选项。
特殊情况
当题目中要求a与b必须为整数,而当a=b求解出a与b又为非整数时,如何处理呢?只要使得a与b尽可能接近即可,其他结论保持一致。
例3
长方形广场的周长为18米,求该广场的面积最大是多少平方米?(该广场的长和宽必须为整数米)( )
A.14B.16C.20D.22.25
【答案】C【解析】设长方形广场的长为a,宽为b,则2×(a+b)=18,可得a+b=9,求广场的最大面积为ab。根据均值不等式的结论:和定差小积大,即a+b=9一定,当a=b=4.5时,ab有最大值为20.25。但已知长和宽为整数米,所以当a与b尽可能接近时,即a=4,b=5时,ab有最大值为20,所以广场的面积为20平方米。故正确答案为C。








