行测技巧：巧用方法解决行测利润问题
利润问题，从“小本买卖”学起
行测数量关系中经常考查利润问题，其重要性不言而喻。今天教大家从一场小本买卖看清利润问题！
一、从小本买卖看计算关系
张大爷爱好养鱼，现在以2元一条的价格购入。李大爷登门拜访，对小鱼甚是心喜，就打算向张大爷买。张大爷报价10元一条。李大爷大砍价，以5元一条买回了家。
这个小故事当中，对于张大爷而言，就像是做了一场小本买卖，一条小鱼成本是2元，标价是10元，实际售价是5元，赚得利润是5-2=3元，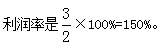
虽然钱数不多，但是利润率很高啊。原价10元，实际售价5元，相当于打折，
就是五折。此时我们学习了三个公式：
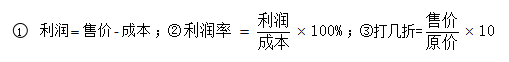
那如果李大爷买走的不是一条鱼，而是以5元的单价买走了六条鱼，此时张大爷从这6条鱼中赚了多少呢？一条赚3元，六条赚18元。所以这就是一个新的计算关系：
总利润=单件利润×销量
二、总结
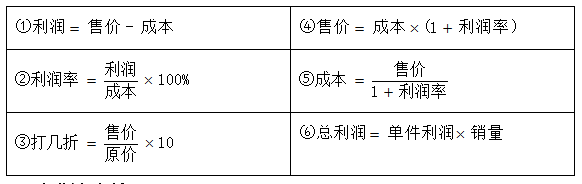
三、经典例题解析
例题1：某商品按定价出售，每个可获得60元的利润。按定价打八折出售10个所获得的利润，与按定价每个减价30元出售15个所获得的利润相同。该商品的定价为多少元？（ ）
A.75 C.80 B.85 D.90
【答案】A【解析】本题给出了明确的描述“按定价打八折出售10个所获得的利润，与按定价每个减价30元出售15个所获得的利润相同”，由此我们得到两种销售情况的总利润相等。第一种情况，定价x元，因为原定价每个可获利60元，所以成本为x-60元。打八折售价为0.8x，单件利润=售价-成本=0.8x-（x-60）=60-0.2x。销售10件，总利润=单件利润×销量=（60-0.2x）×10；第二种情况，每个减价30元，则原来60元的利润少30元，单件利润为（60-30）=30元。销量15件，总利润=单件利润×销量=30×15=450元，因为两种情况总利润相等，所以列出方程（60-0.2x）×10=450，解得x=75，选A。
例题2：小李四年前投资的一套商品房价格上涨了50%，由于担心房价下跌，他将该商品房按市价的9折出售，扣除成交价5%的相关交易费用后，比买进时赚了56.5万元。那么，小李买进该商品房时花了多少万元？（ ）
A.200 B.300 C.250 D.350
【答案】A【解析】设买进成本x万元，上涨50%则市场价1.5x，9折出售则成交价0.9×1.5x，“扣除成交价5%的相关交易费用”说明成本当中包括了5%×0.9×1.5x的交易费，而赚了56.5万元，售价-成本=利润，列式0.9×1.5x-（x+5%×0.9×1.5x）=56.5，解方程得x=200，选A。
利润问题，往往需要我们把买卖的钱数关系梳理清楚，最后依据等量关系求解。
列表梳理复杂利润问题
行测数量关系经常会涉及利润问题的考查，而利润问题是令很多考生无从下手的题目，一方面是因为公式太多，另一方面题目一般数据较多，看起来比较复杂，遇到这种复杂的利润问题，该怎么梳理解题呢？那么接下来带领大家学习一种相对简便的梳理方法——列表梳理复杂利润问题。
基本公式
遇到复杂利润问题时，可以通过列表梳理各个量间的关系，若销量均以比值出现，则可设销量为特值来优化解题步骤，如下：
典型例题
服装店买进一批童装，按每套获利50%定价，卖出这批童装的80%后，按定价的八折将剩下的童装全部卖出，总利润比预期减少了390元。问服装店买进这批童装花了多少元？（ ）
A.5500 B.6000 C.6500 D.7000
【答案】C【解析】设这批童装的成本为x元/套，服装店买进了100套童装。根据题意列表格如下：
预期利润为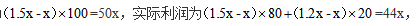
根据“总利润比预期减少了390元”可得，
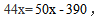解得x=65，故服装店买进这批服装花费
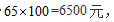本题选择C项。
巧用“特值法”
在行测考试中，数量关系属于非常重要的一个板块，也是各位考生备考的重中之重。从考点来看利润问题是一类高频考点。从难度角度来说，利润问题整体难度适中，属于各位考生要拿分的题型。对于部分利润问题我们可以采用特值法来解题。
根据公式，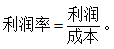
从数学角度各位不难发现，利润率是利润与成本做除法得来；简而言之，利润率是利润与成本的比值，它是一个相对数。
那接下来大家记住一个结论：在数学问题中，如果说已知条件均为相对数（或称之为比值），所求的还是一个相对数（或称之为比值），我们即可用特值解题。
我们一起来看几道例题：
例1：某商店购进一批篮球，定价为进价的125%，在售出进货量的20%后，商店决定打折促销。篮球全部卖完后，商家在该批篮球上总获利15%，问该商店这次促销价为定价的多少折？（ ）
A.8 B.8.5 C.9 D.9.5
【答案】C【解析】观察条件，发现已知条件均为相对数，所求仍为相对数，符合特值法应用条件。不妨假设定价100元，总购进数量为10个。打折后促销价为x元。
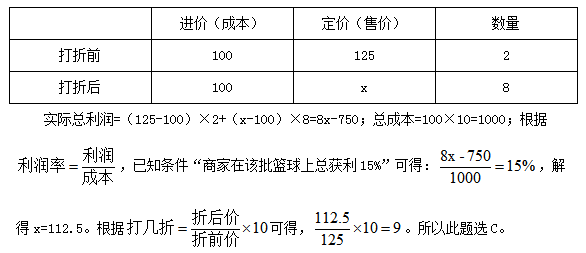
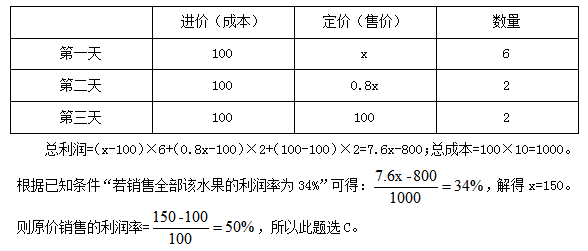
例2：超市销售某种水果，第一天按原价售出总量的60%，第二天原价打八折售出剩下的一半，第三天按成本价全部售出。若销售全部该水果的利润率为34%，则该水果按原价销售的利润率为：（ ）
A.68% B.51% C.50% D.36%
【答案】C【解析】观察条件，发现已知条件均为相对数，所求仍为相对数，符合特值法应用条件。不妨假设成本为100元，原价为x元，水果总量为10个。根据题意可得：
巧用方程法
在行测考试中，数量关系实际上我们在考场上是可以留有一部分时间去挑选一些较简单的题目去做的，从而提升分数。而利润问题，其实就是一类简单的题目。利润问题是研究成本、售价、利润、利润率、打折、销售额等概念之间计算关系的一类问题，可通过基本公式构造等量关系即可求解。
一、基本公式
二、基本方法——方程法
1.设成本为未知数，一般与利润或者利润率相关。
2.设原价或定价为未知数，一般与打折相关。
三、经典例题
【例题1】商品甲的定价是成本的125%，商品乙的定价是275元，成本是220元，现在商店把1件商品甲和2件商品乙配套出售，并且按照它们的定价之和的90%作价出售，这样每套可获得利润80元。商品甲的成本是多少元？（ ）
A.180 B.190 C.200 D.220
【解析】选择C。根据题意，假设甲的成本为x元，那么可列式为：0.9×（1.25x+2×275）-（x+220×2）=80，解得x=200，故本题选择C项。
【例题2】一种设备打九折出售，销售12件与原价出售销售10件时的获利相同。已知这种设备的进价为50元/件，其他成本为10元/件。问如果打八折出售，1万元最多可以买多少件？（ ）
A.80 B.83 C.86 D.90
【解析】选择B。由题意知，该设备的总成本为50+10=60元/件，设该设备原售价为x元，根据题意可列方程为12×（0.9x-60）=10×（x-60），解得x=150，打八折出售时1万元可买10000÷（150×0.8）=83.X件，即最多可买83件。故本题选择B项。
