
行测数量关系常考题型解题技巧
行测数量关系:巧解直角三角形,稳定结构稳定拿分
公务员考试中几何问题考查的频率越来越高,其中解直角三角形则是重中之重。直角三角形作为大家从小就开始接触的知识点,想必对于它是十分亲切熟悉的,因而也成为我们数量关系做题当中的优先选择。那么我们要怎么依据直角三角形的相关知识进行解题呢?
想要能够求解出直角三角形的相关题目,两个相关的知识点是大家需要掌握的。
一、勾股定理:勾股定理指的是直角三角形中两直角边的平方和等于斜边的平方,常见的勾股数有3、4、5;6、8、10;5、12、13;
二、把握含30°和45°角的两个特殊直角三角形的比例关系:含30°的直角三角形中,30°角对应的直角边的长度是斜边的一半,各边之比为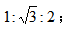 含45°的直角三角形中,各边之比为
含45°的直角三角形中,各边之比为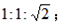 如下图所示:
如下图所示:
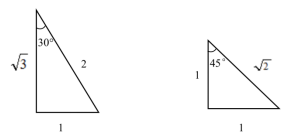
学习了直角三角形的相关知识点,以后再碰到几何问题,我们就可以借助题目条件构造直角三角形,利用勾股定理以及含30°和45°角的直角三角形的各边比例关系来解题,接下来我们就通过两个例题来看看如何求解吧!
例题展示
例题1
甲地在乙地的正东方,在丙地的正南方。甲、乙之间距离为2.1千米。小张从甲地骑车直线前往丙地,回程时以相同速度直线前行乙地再直线返回甲地,回程时的路程比去程长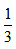 问:甲丙之间的距离在以下哪个范围内?
问:甲丙之间的距离在以下哪个范围内?
A.不到5千米 B.5-6千米 C.6-7千米 D.超过7千米
【答案】D【解析】根据题意,我们可以根据“上北下南,左西右东”的原则画出甲、乙、丙之间的位置关系,如下图所示
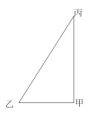
因为甲在乙的正东,在丙的正南,正东和正南构成直角,因而甲、乙、丙三地的连线构成了直角三角形,甲乙之间距离为2.1千米,小张先从甲地到乙地,回程时是由丙→乙→甲,根据回程时的路程比去程长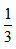 我们可以得到,
我们可以得到,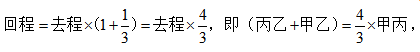 设甲丙之间的距离为3x,那么丙乙+甲乙=4x,丙乙=4x-2.1,根据直角三角形中勾股定理可得
设甲丙之间的距离为3x,那么丙乙+甲乙=4x,丙乙=4x-2.1,根据直角三角形中勾股定理可得 超过7千米。故本题选D。
超过7千米。故本题选D。
例题2
一艘巡逻艇航行至海面某处时,得知正北方向20海里处有一渔船发生故障,就立即指挥港口的救援艇前往该处营救。已知发生事故处位于港口北偏东45°的方向上,港口位于巡逻艇北偏西30°的方向上。港口到出事地点的距离为:

【答案】B【解析】根据题意画出巡逻艇、故障发生处、港口之间的位置关系,如图所示,B点为巡逻艇所在位置,C点为事发地点,A点为港口
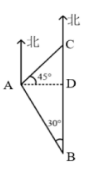
根据题意可知,BC=20海里,∠B=30°可构造直角三角形来解题,过点A作AD垂直于BC,交BC于点D,则∠CAD=90°-45°=45°,设CD=x海里,则AD=CD=x海里,在直角三角形ADB中,由∠B=30°可知,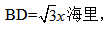 BD+CD=BC,
BD+CD=BC,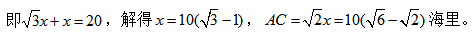 故选B。
故选B。
通过以上两个题目我们可以看到,只要把握住勾股定理和两个特殊直角三角形三边的比例关系这“一定理两特殊”,许多几何问题都可以通过构造直角三角形迎刃而解,大家也可以通过练习更多题目从而能够对于直角三角形的知识点进行灵活应用。
行测年龄问题不用愁,表格梳理来解忧
争分夺秒巧复习,勤学苦练创佳绩。正在备战公考的小伙伴们,你们是否已经做好披荆斩棘的准备?还是苦于找不到自己的练习之路,正处于漫漫摸索的阶段呢?无论进度如何,想必大家都有一些困惑,例如行测考试中的数量关系部分,数学题目难度较高、耗时较长,那如何尽可能在短时间内得出正确结果?今天,带大家认识一种数量关系题型——年龄问题。
年龄问题是研究两个或多个个体之间年龄变化和关系的问题。题目条件易于理解,但数据变化较多,易于混淆,因此,我们在解决这类问题时,通常采用“列表法”来梳理并分析题干,再依据等量关系列方程即可。
那具体该如何列表,请看以下例题:
例题1
一家三口,父亲的年龄比母亲大10岁,2009年,父亲的年龄是儿子的9倍,2016年,母亲的年龄是儿子的3倍,则母亲的出生年份为:
A.1973年 B.1975年 C.1983年 D.1985年
【答案】C解析】假设2016年儿子的年龄为x,则母亲的年龄为3x,父亲的年龄为3x+10。

根据题意可得:9×(x-7)=3x+10-7,解得x=11,母亲2016年为33岁,出生于2016-33=1983年。故选C。
由此可见,我们只需将不同年份下所有人的年龄梳理在表格中,年龄问题就可迎刃而解了。同时小伙伴们也要注意,其实年龄问题中有一个“隐藏福利”,那就是“年份差=个人增加或减少的年龄”,如2009年到2016年,三人的年龄都增加了七岁,同学们可不要忽略这个条件呀!
读到这里,大家是不是都有所收获了呢?那就快练习一下吧!
例题2
2018年父亲年龄是女儿年龄的6倍,是母亲年龄的1.2倍。已知女儿出生当年(按0岁计算)母亲24岁,则哪一年父母年龄之和是女儿的4倍?
A.2036 B.2039 C.2042 D.2045
【答案】B【解析】假设2018年女儿的年龄是x岁,则2018年父亲的年龄是6x岁,母亲的年龄是6x÷1.2=5x岁。

已知女儿出生当年(按0岁计算)母亲24岁,即母亲比女儿大24岁,有5x-x=24,解得x=6,故可得2018年三人年龄并填在表中。再过n年,父母年龄之和是女儿的4倍,有36+30+2n=4×(6+n),解得n=21,所以在2018+21=2039年父母年龄之和是女儿的4倍。故选B。
行测数量关系:未知数多不要慌,工程问题用特值
在行测考试数量关系部分中,工程问题是一种常考题型,解决这类题目的核心是利用工作总量、效率和时间三者之间的关系 列方程解决;在往年考察的题目中往往会出现多者合作完成工作的情况,其中涉及未知数较多,此时我们可以根据题干的描述,巧妙地利用特值法来解决这类题目,接下来就带领大家一起学习一下最常考察的三种特值法解工程问题的题型。
列方程解决;在往年考察的题目中往往会出现多者合作完成工作的情况,其中涉及未知数较多,此时我们可以根据题干的描述,巧妙地利用特值法来解决这类题目,接下来就带领大家一起学习一下最常考察的三种特值法解工程问题的题型。
一、已知多个主体完工时间时,可设工作总量为完工时间的公倍数
例题1
一项工程,甲单独做24天可以完成,甲、乙合作15天可以完成,乙、丙合作10天可以完成。现甲、乙、丙三人合作,3天后有一人有事离开,问最少还需要多少天完工?
A.5 B.6 C.7 D.8
【答案】A【解析】题干中给出了三个完工时间,那么我们设工作总量为24、15和10的最小公倍数120,则甲的效率为120÷24=5,甲、乙的合作效率为120÷15=8,乙、丙的合作效率为120÷10=12,则乙的效率为8-5=3,丙的效率为12-3=9。三人合作3天完成的工作量为3×(5+12)=51,剩余工作量为120-51=69,一人离开后要想工作时间最少,则让效率高的两人继续工作,即甲、丙继续工作,还需69÷(5+9)≈4.9天,因此最少还需要5天可以完工。故本题选A。
二、题干直接给出效率比,可设效率为比例值
例题2
甲、乙、丙三个工程队的工作效率之比为2∶3∶6。一项工程,乙工程队单独施工需要28天完成。实际施工时,甲工程队先单独施工若干天,再由丙工程队单独施工,最终也用了28天完成,则甲工程队完成了工程总量的:
A.30% B.40% C.50% D.60%
【答案】C【解析】题干中直接给出了效率比,那么我们设甲、乙、丙三队的工作效率分别为2、3、6,则工作总量为3×28=84。设实际工作时甲队单独做t天,根据题意有2t+6×(28-t)=84,解得t=21,则甲完成的工作量为2×21=42,故所求为42÷84×100%=50%。故本题选C。
三、题干未给出明确的效率关系,可根据不同工作方式的工作量相等建立等量关系后推出效率关系,再设效率为特值
例3
一批口罩的加工任务,甲单独加工12天完成。若甲先单独加工3天,再由乙单独加工2天,则能完成任务的一半。现甲和乙合作加工若干天后,再由乙单独加工至完成任务,最终发现甲、乙合作加工的时间与乙单独加工的时间相同,则完成该加工任务共用多少天?
A.3 B.4 C.6 D.8
【答案】C【解析】C。根据题意可得, 则甲、乙效率比为2∶3,那么我们设甲和乙的工作效率分别是2和3,则工作总量为12×2=24。设甲、乙合作加工的时间与乙单独加工的时间都是t天,则(2+3)×t+3t=24,解得t=3,故完成该加工任务共用2×3=6天。故本题选C。
则甲、乙效率比为2∶3,那么我们设甲和乙的工作效率分别是2和3,则工作总量为12×2=24。设甲、乙合作加工的时间与乙单独加工的时间都是t天,则(2+3)×t+3t=24,解得t=3,故完成该加工任务共用2×3=6天。故本题选C。
教育希望同学们学习过程中,拿出一些时间有针对性地训练这类题目,从而拿下这一题型。








