政华教育

在行测考试中，资料分析相对而言是考生们比较容易理解和掌握的部分，这部分题目主要是针对考生的材料理解、数据查找、列式计算三方面能力进行考查，许多考生在经过一段时间的学习后往往都能够较好地掌握前两个方面的能力，但是对最后一个列式计算能力方面望而却步，为了能够解决这个问题，提升考生们列式计算的能力，下面政华教育就给大家介绍一种在资料分析里面常用的计算方法：特征数字法。

什么是特征数字法

特征数字法就是利用百分数和分数之间的相互转化，将列式中的百分数近似的转化成一些特定的分数，从而达到方便计算的一种方法。

应用环境

常见的列式类型有：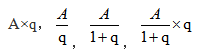

注意事项

我们有时候利用特征数字法进行计算的时候，当选项比较接近的时候，就需要注意答案的放缩：尤其是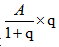的计算中，如果q变大，那么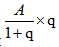也会变大，这时候就需要我们选择偏小的选项。如果q变小，那么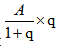也会随之变小，这时候就需要我们选择偏大的选项。

例1:54321×25.4%=（）

A.12356.8 B.14564.8 C.14563.5 D.13797.5

【答案】D【解析】可以将列式中的25.4%近似的看成1/4，那么原式≈54321×1/4=13580.25，由于选项差距较大，选择最接近的答案D选项。

例2：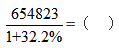

A.495327.5 B.532156.6 C.365641.6 D.446532.9

【答案】A【解析】可以将列式中的32.2%近似看成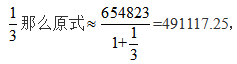由于选项差距较大，选择最接近的答案A选项。

做到这里相信同学们对我们特征数字法有了一定的了解，但是可能部分同学也会冒出一个疑惑，就是自己只知道常见的百分数和分数之间的转换，但是许多不常见的百分数还是不知道该转换为多少，政华教育在此为考生们整理了一下常见的百分数和分数之间的转换表格，希望对大家有所帮助。

常见的百分数和分数之间的转换

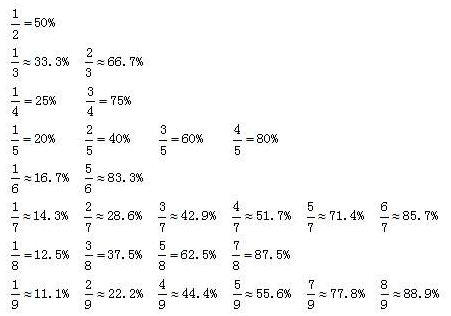
有关特征数字法我们就介绍到这里了，当然所有的方法都需要一个积累、运用的过程，所以要想在考试中能够熟练地运用特征数字法，我们还需要在以后的做题中多加练习。

行测资料分析知识点——常规比率

在行测考试中，资料分析是大家比较容易掌握的部分。资料分析有时候会出现新的概念，出现一些常规比率的材料，增加了阅读与解题的难度，这里做一些

常规比率的介绍，让考生明确此类型知识点考查的本质。

例1：2012年3月份某汽车企业生产汽车63941辆，销售47258辆。

问题：2012年3月份，该汽车企业汽车产销率为多少？

【解析】产销率是指企业在一定时期内已销售出去的产品数量与生产的产品数量之比。即产销率=销售数量/生产数量×100%，代入数据，产销率=47258/63941×100%≈73.9%。

例2：2012年某省规模以上工业企业主营业务收入56730亿元，比上年增长3.5%，增速比全国低7.5个百分点；利润总额2900亿元，比上年下降6.1%。

问题：2012年规模以上工业企业主营业务利润率约为多少？

【解析】利润率反映企业一定时期利润水平的相对指标。利润率指标既可考核企业利润计划的完成情况，又可比较各企业之间和不同时期的经营管理水平，资料分析中考查的利润率是销售利润率，即利润率=利润/收入×100%，代入数据，利润率=2900/56730×100%≈5.11%。

例3：2017年，全国有499.31万普通高中学生享受国家助学金政策。其中，西部地区250.27万人，资助比例32.97%；中部地区180.86万人，资助比例19.70%；东部地区68.18万人，资助比例9.61%。

问题：2017年西部地区申请国家助学金的普通高中学生与中部地区约相差多少万人？

【解析】资助比例是反映研究助学金资助情况的指标。一般指资助人数占申请人数的比重。即资助比例=资助人数/申请人数×100%，现在要求的是申请人数=资助人数/资助比例。代入数据，180.86/19.7%-250.27/32.97%=159万人。

通过以上对一些常规比率的介绍，相信大家已经有些基本了解，我们也可以稍微总结下：一般常规比率也会小于1，分子分母的关系来自生活实际，考试中可以通过对生活的了解来列公式进行计算。

行测资料分析：对外贸易之顺逆差

纵观各类行测考试，资料分析几乎成为必考题型。而在资料分析的材料中，经常会出现对外贸易相关的材料，掌握好对外贸易相关的知识点，有助于我们备考资料分析。现在带着大家一起来了解对外贸易中的顺差和逆差！

什么是顺差？逆差？

对外贸易亦称“进出口贸易”，是指一个国家(地区)与另一个国家(地区)之间的商品和劳务的交换。这种贸易由进口和出口两个部分组成。

当出口额大于进口额时，称为贸易顺差；反之，当进口额大于出口额时，称为贸易逆差。

由于同学们在记忆顺差逆差时容易混淆，所以政华教育给大家一个记忆的小技巧：出口额大的时候，挣钱比较多，挣钱多就顺利，因此出口大的时候为顺差。

核心公式:

顺差=出口额-进口额

逆差=进口额-出口额

公式补充：

进出口总额=出口额+进口额

出口额=(进出口总额+顺差)÷2=(进出口总额-逆差)÷2

进口额=(进出口总额-顺差)÷2=(进出口总额+逆差)÷2

经典例题

例1：2017年全年，上海口岸货物进出口总额79211.40亿元，比上年增长15.1%。其中，进口33445.10亿元，增长18.9%；出口45766.30亿元，增长12.5%。全年上海关区货物进出口总额59690.24亿元，比上年增长14%。其中，进口24684.20亿元，增长19.3%；出口35006.04亿元，增长10.6%。

问题：2017年全年，上海口岸货物进出口贸易顺差比同期上海关区顺差：（）

A.低不到0.3万亿元

B.低0.3万亿元以上

C.高不到0.3万亿元

D.高0.3万亿元以上

【答案】C【解析】2017年全年，上海口岸货物进口33445.10亿元，出口45766.30亿元；全年上海关区货物进口24684.20亿元，出口35006.04亿元。根据公式可得，2017年全年，上海口岸货物进出口贸易顺差=45766.3-33445.1≈12321亿元，上海关区货物进出口贸易顺差=35006.04-24684.2≈10322亿元，故差值=12321-10322≈2000亿元=0.2万亿元，故正确答案为C。

例2：2014年上半年，全省累计完成外贸进出口总值125.39亿美元，同比增长2.2%，高于全国平均增速1.0个百分点。其中，出口总值26.79亿美元，同比下降20%；进口总值98.61亿美元，同比增长10.6%。

问题：2013年上半年，E省外贸进出口总值顺差(+)或逆差(-)为多少亿美元9 ？

A.+55.67 B.-55.67 C.+125.4 D.-125.4

【答案】B【解析】2013年上半年进出口总值差值=2013年上半年出口总值-2013年上半年进口总值=26.79÷(1-20%)-98.61÷(1+10.6%)≈34-90=-56，即进口大于出口，称为逆差。与B项最接近，故正确答案为B。

行测资料分析：快速判定比重增长量看这里

比重增长量是资料分析里比较常见的题型，但也成为了很多同学的难题，其实这类题目看起来计算量很大，但只需要简单计算并结合选项排除错误选项，就可以快速锁定答案。

题型识别

比重增长量本质依然是增长量，增长量=现期值-基期值，那么比重增长量=现期比重-基期比重。这类题目常见的问法都是：某个时间A占B的比重与基期时间A占B的比重相比是上升还是下降？或者是会问上升还是下降了多少个百分点？即出现：两个时间对比+比重+上升/下降+百分点。

计算公式

比重增长量公式：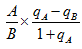

A：部分值现期值 B：整体值现期值

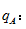部分值增长率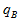：整体值增长率

判定比重上升/下降依据

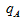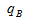>，现期比重大于基期比重，比重上升；

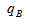<，现期比重小于基期比重，比重下降；

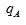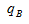=，现期比重等于基期比重，比重不变。

例1：2019年，全国水产品总产量6480.36万吨，比上年增长0.35%。其中，养殖产量5079.07万吨，同比增长1.76%。

问题：2019年全国水产品总产量中，养殖产量所占比重较上年：（）

A.上升 B.下降 C.持平 D.无法判断

【答案】A【解析】根据题干，需要判断“2019年……比重比2018年比重上升/下降”，因此只需要比较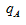与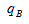的大小关系。同时根据“占”字确定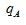，表示养殖产量的增长率，为1.76%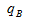，表示全国水产品总产量的增长率，为0.35%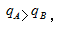，比重上升。正确答案为A。

例2：2019年，全国地勘单位在职职工41.43万人，较上年增加5.37%。其中，工程勘察与施工人员7.46万人，较上年增加17.67%

问题：2019年，全国工程勘察与施工人员数占全国地勘单位在职职工数的比重较上年约：（）

A.上升1.9个百分点 B.上升19个百分点

C.下降1.9个百分点 D.下降19个百分点

【答案】A【解析】根据题干“2019年的……比重，较上年”，并且结合选项“上升/下降+百分点的单位”，可判定本题为比重的增长量问题。根据公式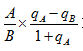求比重的增长量，同时通过“占”字确定：A表示“全国工程勘察与施工人员数”，为7.46万人；B表示“全国地勘单位在职职工数”，为41.43万人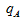；表示A对应的增长率，为17.67%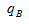；表示B对应的增长率，为5.37%。所有数据代入公式为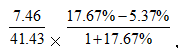：观察选项，两个上升，两个下降，因为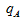（17.67%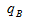）＞（5.37%）则比重上升，排除C、D；又因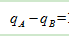=17.67%-5.37%=12.3%接下来12.3%要除以“1+17.67%”这个大于1的数，然后再去乘前面现期比重，现期比重都是小于1的数，所以结果一定比12.3%(化成百分点形式12.3个百分点)要小，因此正确答案为A。

比重增长量题目看似复杂，但是我们通常可以直接先去观察并计算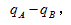确定比重上升或下降，排除错误选项，然后再根据简单的估算，选出正确答案。

行测资料分析：多几倍和增长率傻傻分不清楚

增长和倍数都是资料分析中常考的考点，在梳理材料时我们总会遇到某一个统计指标增长百分之几或者多几倍这样的描述，总是感觉这两者之间应该有点关系，但到底是什么关系呢，今天政华教育带大家来一探究竟。

例题：2020年北京软件行业业务收入为15677.4亿元，2014年为4796.6亿元。

问题①：2020年北京软件行业业务收入比2014年增长了百分之几？

题干中2020年与2014年比较，则2020年为现期，2014年为基期，现在已知现期值和基期值，求增长率，因此列式为：

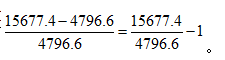
问题②：2020年北京软件行业业务收入比2014年多几倍？

题干求的是多几倍，根据比字确定2020年的值为分子，2014年的值为分母，因此列式为：多几倍=是几倍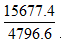-1=-1。

观察发现，问题①与问题②的最终列式一模一样，因此我们得出：增长率=多几倍。在一篇资料中，当增长率小于100%时，我们习惯用百分数来表示；当增长率大于100%时我们习惯用多几倍来表示。例如增长率为35%时，表示为增长了35%，当增长率为130%时，表示为增长了1.3倍或多了1.3倍。

例题：2014年上海艺术表演团体机构数为158个，比2008年多2.8倍。

问题①：2008年上海市艺术表演团体机构数为多少个（）？

A.56 B.42 C.32 D.28

【答案】B【解析】根据材料中2014年比2008年可知，2014年为现期，2008年为基期，现已知现期值为158个，比2008年多2.8倍即增长率为2.8，求基期值，则列式为故答案为B。

问题②：2014年上海市艺术表演团体机构数比2008年多多少个（）？

A.95 B.105 C.116 D.126

【答案】C【解析】已知现期值为158个，增长率为2.8，求解增长量，则列式为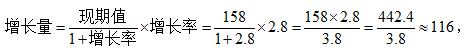故答案为C。

通过这道例题我们发现，当题干中出现多几倍、高几倍、增长几倍的时候，我们就把它当作增长率来用，带入到增长的公式中，从而解题即可。