政华教育

【解析】“企业列出500万元设备采购预算，如用于购买x台进口设备，最后剩余20万元”也就是给了500万减去购买进口设备的钱数等于20万这样一个等量关系，购买设备的金额需要用设备台数x乘进口设备的单价，那不妨假设进口设备的单价为a万元/台，那可以列式为：500-xa=20，又说“决定购买质量更高的同类国产设备，单价仅为进口设备的75%”那国产设备的单价即为0.75a。“当前预算可购买x+3台，最后剩余5万元”也就是说500万减去购买国产设备的金额等于5万，那么同理我们来列式：500-(x+3)×0.75a=5，问题问国产设备的单价在以下哪个范围内？求的是0.75a。我们回到式子中，有两个方程有两个未知数，可以求解出结果，整理求解得到0.75a=45，结合选项选择C。

例题2

为降低碳排放，企业对生产设备进行改造，改造后日产量下降了10%，但生产每件产品的能耗成本下降了50%，其他成本和出厂价不变的情况下每天的利润提高了10%。已知单件利润=出厂价-能耗成本-其他成本，且改造前产品的出厂价是单件利润的3倍，则改造前能耗成本为其他成本的：（）

【答案】B

【解析】梳理一下题干，“设备进行改造，改造后日产量下降了10%”假设改造前的日产量为a，那改造后的就为0.9a。又说“生产每件产品的能耗成本下降了50%，其他成本和出厂价不变”说明成本就分为能耗成本、其他成本。能耗成本下降50%，假设之前的能耗成本为b，那之后的能耗成本就为0.5b。其他成本和出厂价不变的情况下，每天的利润提高10%，也就是说有现在每天的利润=原来每天利润×(1+10%)这样一个等量关系，而每天的利润就应该等于日产量乘单件利润，改造前后的日产量都已经表示出来，所以需要寻找改造前后的单件利润。而题目中给了一个关于单件利润=出厂价-能耗成本-其他成本的等式，又说改造前产品的出厂价是单件利润的3倍，假设之前的单件利润为c，那之前的出厂价就为3c，根据等式可得：其他成本=出厂价-能耗成本-单件利润，即为3c-b-c=2c-b。而改造后其他成本和出厂价不变，那改造后其他成本也为2c-b，出厂价也为3c，那么我们想要的改造后的单件利润就能表示出来，为3c-0.5b-(2c-b)=c+0.5b，关于每天利润的等量关系就可以表示为：0.9a(c+0.5b)=ac×1.1。最后问改造前能耗成本为其他成本的多少，即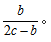那简单整理下方程，发现等式两边都有a，可以约掉，整理得到0.2c=0.45c，再观察下所求的为2c和b的关系，将0.2c=0.45b，整理为2c=4.5b带进去约分，就得到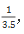结合选项，选B。

知识小结

我们会发现利润问题公式会有很多，其实公式多也就意味着等量关系会有更多，入手点更多，我们在选择入手点时可以选择一些也复合概念，比如例题2，以每天利润=日产量×单件利润这个复合概念来列式。当然只要把握好核心观念找等量关系，勤加练习类似题型，会更快掌握此类题型。

行测统筹问题指导之空瓶换水

近年来，统筹问题已成为行测考试中的“新宠儿”，例如在我们日常生活中经常遇到的空瓶换水、货物集中、排队取水等。面对这类问题，我们该如何合理安排，从而更高效地办事呢？这其实就是我们要在统筹问题中去解决的。而空瓶换水问题作为统筹问题中的一类，各位考生总是对此心有余悸。接下来将通过两道例题带领大家一起来突破这道难关。

概念

空瓶换水，指的是给出n个空瓶可以换1瓶水的规则，问现有的空瓶最多可以换多少瓶水，或者要想喝到一定数量的水，问最少需要购买多少瓶水等类似的问题。

考法

1.直接套用规则：已知规则和空瓶数，求最多能喝到的瓶数。

例1：一商店规定4个矿泉水空瓶可以换1瓶矿泉水，现有27个矿泉水空瓶，则最多可以换( )瓶矿泉水。

A.6 B.7 C.8 D.9

【答案】D【解析】当矿泉水瓶数量较小的时候，我们可以按规则一步一步地进行兑换。但在实际考试过程中，这种方法不仅浪费时间而且容易在兑换过程中出现差错，这并不能满足我们解决行测问题的快、准原则。那我们该如何去计算呢？下面政华教育为大家提供一种更好的解题思路。

根据题干中的“4个矿泉水空瓶换1瓶矿泉水”，我们用等式来表示就可以写成：4个矿泉水空瓶=1瓶矿泉水=1个矿泉水空瓶+1份水(一份水不包括空瓶)，可以得：3个矿泉水空瓶=1份水。现在我们用27÷3=9，即27个矿泉水空瓶通过兑换最多可以得到9瓶水。答案选D。

总结：通过这个例题发现，在解决空瓶换水问题时，我们只需要找到空瓶与水的代换关系，即n个空瓶可以换1份水，然后用总的空瓶数m来除以n就可以得到最终答案。

2.间接套用规则：已知规则及喝到的瓶数，求至少应买多少瓶水。

例2：商店做活动，8个空瓶可以换一瓶水，小芳这个月一共喝了65瓶水，那么她花钱买的至少有多少瓶水？（）

A.56 B.57 C.58 D.59

【答案】B【解析】首先我们需要注意，小芳喝的这65瓶水包括小芳她自己花钱买的和通过兑换得到的。因此，如果我们设小芳花钱买了x瓶水，并且题干中的“8个空瓶可以换一瓶水”，我们用等式来表示可以写成：8个矿泉水空瓶=1瓶矿泉水=1个矿泉水空瓶+1份水(一份水不包括空瓶)，可以得：7个矿泉水空瓶=1份水。则小芳通过兑换可以得到x÷7瓶水，因此可以得到x+x÷7=65，解得x=56.875，即至少买56.875瓶水加上兑换的才能保证小芳这个月喝了65瓶，而矿泉水瓶数只能是整数，因此在不小于56.875的整数里选择最小的57，答案选B。

总结：当我们已知规则及喝到的瓶数，求至少应买多少瓶水时，我们只需要利用换水规则列方程求解即可。只不过需要注意的是，当未知数解出来为非整数时，我们需要向上取整。

学到这里，大家对空瓶换水问题是不是很清晰明了了呢？在遇到空瓶换水问题时，我们只需抓住空瓶换水的规则便可以快速解题。希望通过今天的分享能为各位考生在备考路上起到一定的助力作用。

你知道A事件发生的概率是多大吗

概率问题是国省考行测中的重要题型，也让很多考生为之头疼，是大家的痛点和难点，但解决这类题型的思路和方法相对固定，有很强的规律性。今天就带大家学习概率问题的求解方法，让大家遇到这类问题能够很好地解决。

公式

概率研究某一事件发生的可能性大小。在行测考试中常考古典概率(又称等可能事件概率)，强调事件具有有限性以及每个基本事件发生的可能性相等。求解A事件发生的概率：想得知概率为多大，就得找到“总事件包含的等可能样本数”以及“A事件包含的等可能样本数”，找到这二者，概率问题也就迎刃而解。

实战演练

例1：小王从编号分别为1、2、3、4、5的5本书中随机抽出3本，那么，这3本书的编号恰好为相邻三个整数的概率为多少？（）

【答案】C【解析】所求概率为多少，根据概率计算公式，找到“总事件所包含的等可能样本数”以及“A事件包含的等可能样本数”。总事件为从5本书中随机抽出3本，故总事件有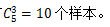所求A事件为选出3本书的编号是相邻的三个整数，符合条件的有1、2、3，2、3、4，3、4、5，有3个样本。故所求概率为。选C。

例2：从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？（）

A.10% B.30% C.60% D.90%

【答案】D【解析】所求概率为多少，根据概率计算公式，找到“总事件所包含的等可能样本数”以及“A事件包含的等可能样本数”。总事件为从5个数中随机抽出3个数，故总事件有所求A事件为3个数之和至少能被其中一个数整除，由于任何整数都能被1整除，故可以分类讨论，当抽取的3个数中含有1时，还得从剩下的4个数中抽取2个，每一个基本事件都能满足3个数之和至少能被其中一个数整除的条件，故样本数为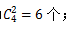当抽取的3个数中不含有1时，就得从剩下的2、3、4、5中抽取3个数，样本数较少，可以一一讨论，分别为2、3、4，2、3、5，2、4、5，3、4、5，抽取的3个数为2、3、4时，和为9，能被3整除，满足条件，抽取的3个数为2、3、5时，和为10，能被2和5整除，满足条件，抽取的3个数为2、4、5时，和为11，不满足条件，抽取的3个数为3、4、5时，和为12，能被3和4整除，满足条件，故样本数为3个；因此所求A事件的样本数为6+3=9个。所求概率为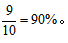选D。

小结：解决古典概率问题，得明确总事件以及所求的A事件是什么，从而求出其对应的基本事件样本数，带入求解得到概率。

希望各位小伙伴通过上面两道能够掌握古典概率在具体题目中的运用，对做题带来一定的启发。

用特值法解决工程问题中的多者合作

很多同学认为行测数量关系做起来很花时间且有一定的难度，从而不大愿意去花时间拿分，在这里给大家分享一种可以拿分的题型，即工程问题下的多者合作题型。工程问题是考场上常见的一种题型，这种题型一般情况下都是用方程来解，但速度不够快，如何能够做到做对的同时又保证做题的效率呢？接下来给大家具体介绍一下它的用法。

基本公式

工作总量=工作效率×工作时间

基本方法

1.当题目中出现多个完成工作时间，设工作总量为特值，一般为时间的最小公倍数。

例1：录入员小张和小李需要合作完成一项录入任务，这项任务小李一人需要8小时，小张一人需要10小时。两人在共同工作了3个小时后，小李因故回了趟家，期间小张一直在工作，小李返回后两个人又用了1个小时就完成了任务。在完成这项任务的过程中，小张比小李多工作了几个小时？（）

A.1 B.1.5 C.2 D.2.5

【答案】A【解析】设工作总量为40(8和10的最小公倍数)，则小李的工作效率为5，小张的工作效率为4。由题意可知，两人合作了3+1=4小时，完成工作量(4+5)×4=36，则小张单独工作(40-36)÷4=1小时，即小张比小李多工作了1小时。

2.当题目中出现效率比，设效率比为特值。

例2：甲工程队与乙工程队的效率之比为4∶5，一项工程由甲工程队先单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多：( )。

A.3天 B.4天 C.5天 D.6天

【答案】C【解析】设甲、乙工作效率分别为4、5，则这项工程的任务量为4×6+5×8+(4+5)×4=100。甲工程队单独完成需要100÷4=2天，乙工程队单独完成需要100÷5=20天，所求为25-20=5天。

3.当题目中出现多人或多物，设效率为1。

例3：修一条公路，假设每人每天的工作效率相同，计划180名工人1年完成，工作4个月后，因特殊情况，要求提前2个月完成任务，则需要增加工人多少名？（）

A.50 B.65 C.70 D.60

【答案】D【解析】设每名工人每月的工作量为1，则全部工作量为180×12，工作4个月完成工作量180×4。设要想提前2个月，则需要增加工人x名，则有180×4+(180+x)×(12-4-2)=180×12，解得x=60。

相信大家通过上面三个例题，能对多者合作下的特值法有一定的理解，特值法的应用范围还是能够保质保地去解决题目，建议接下来各位同学在做题的过程当中能去使用这种方法，真正掌握这种做题的方法，从而提高自身的做题水平。