
公务员考试行测备考--数量关系
行程图巧解行程问题
公务员考试行测备考走进行程问题,利用行程图巧妙的解答,把行程问题的分值收入囊中。
【公式法】
若题干等量关系明确,直接求解。即可通过基本公式:路程=速度×时间直接求解。
例题:货车早上8点出发,以60千米/小时的速度匀速驶往40千米外的货场装运货物,装运结束以后以去时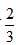 的速度匀速返回,并于正午12点到达,那么货车装运货物的时间是其在路上行驶时间的几倍?
的速度匀速返回,并于正午12点到达,那么货车装运货物的时间是其在路上行驶时间的几倍?
A.1 B.1.4 C.1.5 D.1.8
答案解析:两地相距40千米,去时速度为60千米/小时,可得去时用了40÷60= 小时,回程速度为60×
小时,回程速度为60× =40千米/小时,则回程所用时间为40÷40=1小时,可得货车行驶的总时间为
=40千米/小时,则回程所用时间为40÷40=1小时,可得货车行驶的总时间为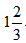 小时,而总时间为4小时,则装运货物时间为
小时,而总时间为4小时,则装运货物时间为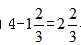 小时,因此所求为
小时,因此所求为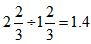 倍。选择B选项。
倍。选择B选项。
【行程图法】
若运动过程复杂时,可借助行程图求解。画行程图时利用“路程”建立等量关系。
例1:邮递员骑自行车从邮局到渔村送邮件,平常需要1小时,某天在距离渔村2公里处自行车出现故障,邮递员只好推车步行至渔村,步行速度只有骑车的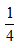 ,结果比平时多用22.5分钟,问邮局到渔村的距离是多少公里?
,结果比平时多用22.5分钟,问邮局到渔村的距离是多少公里?
A.16 B.17 C.18 D.19
答案解析:设平常邮递员骑车的速度为v公里/小时,t小时时自行车出现故障,22.5分钟=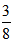 小时,结合题意作图如下:
小时,结合题意作图如下:
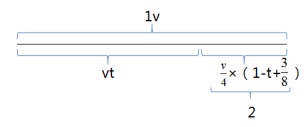
根据图中线段关系可得,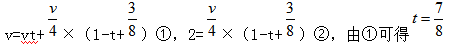 ,代入②解得 v=16,因此邮局到渔村的距离是16×1=16公里。选择A选项。
,代入②解得 v=16,因此邮局到渔村的距离是16×1=16公里。选择A选项。
例2:甲乙二人上午8点同时从东村骑车到西村去,甲每小时比乙多骑6千米,中午12点甲到达西村后立即返回东村,在距西村15千米处遇到乙,东西两村相距多远?
A.62 B.61 C.60 D.59
答案解析:设甲的速度为v千米/小时,则乙的速度为(v-6)千米/小时,甲到达西村后又走了t小时与乙相遇,结合题意作图如下:

根据图中线段间的关系可得,4v=4×(v-6)+(v-6)t+vt①,vt=15②。解得 t=1,v=15,故东、西两村相距 15×4=60 千米。选择C选项。
同学们在利用行程图解行程问题时一定要谨记,标注数据时统一标注为“路程”。如果题干中没有直接表述路程的具体数据,可通过路程=速度×时间来表示,遇到未知量可设为未知数,即某段路程可用vt来表示。利用行程图中同段路程相同来建立等量关系,不要惧怕未知数较多,计算时可进行消元。对于行程图法需多加练习,准确无误的选择答案。
方阵问题中的小规律
在公务员考试中行测数量关系的这一部分有一种独特的数学模型我们称之为“方阵问题”,这类题目在实际的考查中相对会比较灵活多变,还是让很多同学望而生畏,但其实只要我们掌握了其中的规律就可以轻松应对。
首先我们要认识什么样的问题才是方阵问题,方阵其实是一种队形,一个队伍排队,横着排叫行,竖着排叫列,若行数与列数都相等,正好排成一个正方形,这种队形就叫做方阵。将一些物体按照这样的方式排列起来,也叫做方阵。方阵分为实心方阵和空心方阵两种,无论是哪种方阵在考试中都是围绕方阵的层数、每层人数、总人数来展开问题的。
方阵问题主要对应以下几条规律,同学们一定要牢记:
1、每层人数=4×(每边人数-1)
2、每层每边人数依次增加2
3、每层总人数依次增加8(行人数为奇数的最内层除外)
4、实心方阵总人数=最外层每边人数的平方
那么具体如何应用呢?实心方阵与空心方阵的区别在哪儿?我们来看下面的例题。
【例题1】若干学校联合进行团体操表演,参演学生组成一个方阵,已知方阵由外到内第二层有104人,则该方阵共有学生( )人。
A.625 B.841 C.1024 D.1369
【答案解析】此题是一个实心方阵的例题,已知由外到内第二层有104人,通过每层总人数依次增加8可知最外层有104+8=112人,又通过每层人数=4×(每边人数-1)可知该方阵最外层每边有29人,所以总人数为29×29=841,故选择B项。
【例题2】同学们排练团体操,排成一个三层空心方阵多出9人,如果在空心部分再增加一层又差7人。问有多少名学生参加了团体操比赛?
A.89 B.93 C.105 D.121
【答案解析】此题是一个空心方阵的例题,根据排成一个三层空心方阵多出9人,如果在空心部分再增加一层又差7人,可知空心方阵再加的一层共16人,根据规律每层总人数依次增加8可知,原来的三层空心方阵每层认识分别为24人、32人、40人,所以总人数为24+32+40+9=105人,故选择C项。
两招解决容斥问题
容斥问题是行测数学运算部分中比较青睐的题型之一,考察的题目不多,难度一般也是中等偏下,是同学们比较愿意看到的题型,所以只需要大家熟悉理论基础,根据题干中的已知条件寻找到合适的解题方法就能够轻松解决。容斥问题的基础理论并不复杂,尽管名字很多人并没有听说过,但并不影响大家的学习,所以同学们不要有畏难情绪,理论基础和解题方法都是理解起来非常轻松的,解题方法并不多,只要理解后根据题型和题干信息锁定方法就解决了,所以同学们解决容斥问题的入手点其实是题目的分析,重点是两种方法的灵敏度和运用熟练程度,只要清楚解题方法的适应条件就能够轻松解题,所以容斥问题是要把功夫花在理论和方法的理解上。
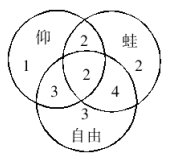
【例题】一次运动会上,18名游泳运动员中,有8名参加了仰泳,有10名参加了蛙泳,有12名参加了自由泳,有4名既参加仰泳又参加蛙泳,有6名既参加蛙泳又参加自由泳,有5名既参加仰泳又参加自由泳,有2名这3个项目都参加,这18名游泳运动员中,只参加1个项目的人有多少?
A.5 名 B.6 名 C.7 名 D.4 名
【答案解析】本题画出文氏图很容易得出结果,需要注意的是有一名运动员没有参加任何一项。所以结果是6名而非7名。
【例题】 某乡镇举行运动会,共有长跑、跳远和短跑三个项目,参加长跑的有49人,参加跳远的有36人,参加短跑的有28人,只参加其中两个项目的有13人,参加全部项目的有9人。那么参加该次运动会的总人数为:( )
A.75 B.82 C.88 D.95
【答案解析】三集合容斥问题,所求为 49+36+28-13-9×2=82。
【例题】在一次调研中,有问卷调研、当面访谈和电话访谈三种形式,其中参与问卷调研的有27人、电话访谈的有21人,三种都参与的有5人,既参与问卷调研又参与当面访谈的有9人,既参与问卷调研又参与电话访谈的有12人,既参与当面访谈又参与电话访谈的有7人,已知,只参与当面访谈的人数占总数的20%,则总共参与调研的有多少人?
A.45 B.50 C.55 D.60
【答案解析】方法一,画出三个集合的文氏图,根据题中条件简单计算依次填充数据,设总人数为x,如下图,可得27+7+2+0.2x=x,解得x=45,选择 A。
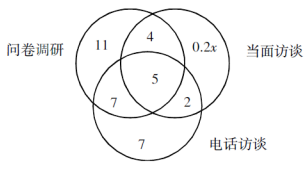
方法二,分析题意,可知总人数相当于参与问卷调研和电话访谈的实际人数,再加上只参与当面访谈的人数。设总人数为x,则有27+21-12+0.2x=x,解得x=45。
通过上述几道例题可以看出,在题干描述中,能够很快锁定题型,但是解题方法却不都是一种,能看到有些题使用公式很快捷,但有些题目使用文氏图分析的更加清晰,更有利于分析和列式。那么应该怎么选择方法呢,同学们只需要记住当所给题目条件非常充分,均是公式中所需数据并且所求是公式中的数据,那么就可以直接列式计算;如果题干描述比较晦涩难懂或者对于所求没有思路时,就使用文氏图进行数据的整理和分析,然后列式计算即可。所以同学们灵活使用两种方法,做到熟练运用,在考试中容斥问题的分数就拿到了。
用“特殊”值解决多者合作问题
很多同学在行测考试中都会将数量关系放在最后的时间去做,一般有两个原因,第一个是因为本身时间就非常有限,同学们会将时间和精力放在相对容易好做的题型中;第二个是因为数量关系确实有些题目是比较难做的,所以很多同学都没有很多时间来做数量关系,那也就要求同学们在做数量关系时要学会挑题,在有限的时间内尽量去挑选一些可以做而且不会花费很多时间的题目来做,其实有一种题目--多者合作问题就是各位同学可以挑选出来去做的。
为什么说可以挑选出来做呢?因为工程问题中的多者合作问题有一个相对好用的方法--特值法,各位同学熟练掌握了特值法之后,在做多者合作问题时就没有那么“头疼”了,特值法是什么意思呢?就是给题干中的某未知量赋特殊值,有三种设特值的方法:
常见题型
1.已知多个主体完工的时间,一般将工作总量设为1或多个完工时间的公倍数
例1:一项工程,甲一人做完需要30天,甲、乙合作完成需要18天,乙、丙合作完成需要15天,甲、乙、丙三人共同完成该工程需要多少天?
A.8天 B.9天 C.10天 D.12天
【答案解析】这道题告诉我们多个主体完工的时间,可以将工作总量设为90(30、18、15的最小公倍数),则甲的效率是3,甲乙效率之和是5,乙丙的效率之和是6,多者合作问题的解题核心是效率可以加和,甲乙丙的效率之和是3+6=9,那么,甲乙丙的合作时间是90÷9=10天,选择C项。
2.已知多个主体效率关系时,一般根据效率关系将效率设为最简比对应的份数
例2:某项工程甲乙丙三人合作6天可以完成。若甲、乙、丙的工作效率比为3∶6∶8,则乙单独完成这项工作需要多少小时?
A.10 B.17 C.24 D.31
【答案解析】这道题已知甲乙丙的效率比例关系,设甲的效率是3,乙的效率是6,丙的效率是8,则工作总量为(3+6+8)×6,即乙单独完成的时间为(3+6+8)×6÷6=17小时,选择B项。
3.已知多个劳动力的效率相同时,一般设每个劳动力的效率为1
例3:一批零件,有3台效率相同的机器同时生产,需用10天完成。生产了2天之后,车间临时接到工厂通知,这批零件需要提前2天完成,若每台机器的效率不变,需要再投入多少台相同的机器?
A.1 B.2 C.3 D.4
【答案解析】这道题已知每台机器效率相同,设每天机器每天工作的效率为1,则工作总量为1×3×10=30,工作2天后工作总量剩30-3×2=24,因为已经工作2天,还剩10-2-2=6天,则每天需要24÷6=4,每天机器每天效率为1,则需要再投入1台,选择A项。
用特值法来解决多者合作问题,多加练习熟练掌握上面这三种设特值的方法,加快做题速度!








