
行测数量关系:“公约数”与“公倍数”问题
“公约数”与“公倍数”问题
一、什么是公约数
如果一个整数同时是几个整数的约数,称这个整数为它们的“公约数”,公约数中最大的称为最大公约数。
二、什么是公倍数
指在两个或两个以上的自然数中,如果它们有相同的倍数,这些倍数就是它们的公倍数。
三、方法与技巧
两个数最大公约数和最小公倍数的求法。
一般采用短除法,即用共同的质因数连续去除,直到所得的商互质为止。
①将共同的质因数连乘起来,就是这两个数的最大公约数。
②将共同的质因数、各自剩余互质的质因数连乘起来,就是这两个数的最小公倍数。
【例】求12和28的最大公约数和最小公倍数
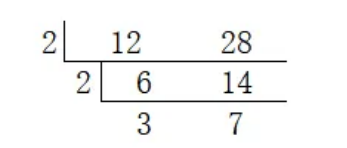
12、28的最大公约数:2×2=4;
12、28的最小公倍数:2×2×3×7=84。
四、例题展示
【例1】有一种红砖,长24厘米、宽12厘米、高5厘米,至少用多少块红砖才能拼成一个实心的正方体( )?
A.600块
B.800块
C.1000块
D.1200块
【答案】D【解析】由题可知,要想拼成正方体,则每条边的长度必须是24、12、5,即120的最小公倍数。此时每条边上需要的砖数分别是5、10、24,因此至少需要红砖为5×10×24=1200块。因此选择D。
【例2】某企业员工编号为6位自然数,其中前两位代表入职年份的最后两位数,第3位代表所属部门,后3位代表员工当年在部门中的入职顺序。2018年入职的员工小张发现,自己的员工编号能同时被5、9和101整除。问当年他所在的部门最少可能有多少人入职( )?
A.不到250人
B.250~499人之间
C.500~749人之间
D.超过749人
【答案】B【解析】由题可知,小张18年入职,那么工号前两位为18。又因为该他的员工编号能同时被5、9、101整除,因此,即为4545的倍数。再者,前两位是18且是4545倍数的六位数只有181800,及其41倍的186345。最后,已知后三位为员工入职顺序,故其部门18年最少有345人入职。因此选择B。
【例3】箱子里有标号为1-10的10个球,小张随机取了三个球并记下号码后将球放回,小李也随机取了三个并记下号码。这时发现两人取的球的号数之积都恰好是144。已知小张的号数之和比小李的大,那么小张取的球的号数之和是多少( )?
A.19
B.17
C.16
D.14
答案】A【解析】由题可知,三个小球的编号乘积均为144,那么对144进行因式分解可得:144=2×2×2×2×3×3。又因小球编号各不相等,则可得144=9×8×2=8×6×3。又因为小张的号码数之和较大,所以之和应为9+8+2=19。因此选择A。
公约数和公倍数的应用
一、概念区分
公约数:某个数是几个整数共同的约数。公约数中最大的称为最大公约数。
公倍数:在两个或两个以上的自然数中,它们之间相同的倍数就是它们的公倍数。这些公倍数中最小的称为这些整数的最小公倍数。
二、根据题目特征判断所考查知识点
公约数
【例1】桌上放有三根绳子,长度分别是120厘米、160厘米、240厘米,现在要把它们截成长度相等的小段,每根都不能有剩余,那么最少可截成多少段( )?
A.13
B.12
C.11
D.10
【答案】A【解析】要保证截成相同长度的小段,每根都不剩余,则每小段的长度必须是120、160、240的约数,要保证截成的小段最少,则每小段的长度应是120、160、240的最大公约数。120、160和240的最大公约数为40,则有120÷40=3,160÷40=4,240÷40=6,所以最少截成3+4+6=13段。故选A。
公倍数
【例2】有一个电子钟,每走9分钟亮一次灯,每到整点响一次铃。中午12点整,电子钟响铃又亮灯。下一次既响铃又亮灯的时刻是多少( )?
A.下午1点
B.下午2点
C.下午3点
D.下午4点
【答案】C【解析】每两次亮灯的时间间隔是9分钟的倍数;每两次响铃的时间间隔是60分钟的倍数。所以,下次既响铃又亮灯的时间间隔是9和60的最小公倍数,为180。则下次既响铃又亮灯是12点整过180分钟,即下午3点,故选C。
三、巩固练习
1.甲、乙、丙三人定期到某棋馆学围棋,甲每隔3天去一次,乙每隔4天去一次,丙每隔5天去一次。若2016年2月10日三人在棋馆相遇,则下次三人在棋馆相遇的日期是:( )
A.4月8日
B.4月11日
C.4月9日
D.4月10日
【答案】D【解析】“每隔3天”即“每4天”,“每隔4天”即“每5天”,“每隔5天”即“每6天”,下次三人在棋馆相遇经过的天数为4、5、6的最小公倍数60。2016年为闰年,2月有29天,从2月11日算起,2月还剩19天,3月有31天,19+31=50,则三人下次在棋馆相遇的日期是2016年4月10日,故选D。
2.若A、B、C三种文具分别有38个、78个和128个,将每种文具都平均分给学生,分完后剩下2个A,6个B,20个C,则学生最多有多少人( )?
A.9
B.12
C.18
D.36
【答案】D【解析】每种文具都平均分给学生,分完后剩下2个A,6个B,20个C,则学生人数是38-2=36、78-6=72、128-20=108的公约数,这三个数的最大公约数是36,因此学生最多有36人。








