行测数量关系解题技巧
“巧用整除速解难题”
在行测试卷中，数量关系部分题目难度相对较高，是很多考生备考的难点，提到总是会犯怵，认为计算问题难解，思维策略题更难想。那么我们要想提高分数，就要在积累基础知识的前提下掌握相应的解题技巧，整除思想就是其中一个。也就是利用数的一些整除特性来快速解决一些比较复杂的题目，能够在节约时间的同时把题目做对。接下来带大家学习一下如何来巧用整除，速解难题。
整除就是一个整数除以另一个整数，商为整数并且没有余数的式子。即a能被b整除，或者说b能整除a，可表示为a÷b=c(a、b、c均为整数)。而数的整除特性可以帮助我们快速排除错误选项，从而达成快速选择准确答案的目的。
下面我们以两个例题来体验一下。
【例1】某单位原拥有中级及以上职称的职工占职工总数的62.5%。现又有2名职工评上中级职称，之后该单位拥有中级及以上职称的人数占总人数的7/11则该单位原来有多少名职称在中级以下的职工（ ）？
A.68 B.66 C.62 D.60
【答案】B【解析】方法一：设职工总数为X人，可得现有中级及以上人数为62.5%X+2；由现有中级及以上占总人数的7/11得，62.5X+2=7/11X，解的X=176(人)。则原来中级以下的职工有176×(1-62.5%)=66(人)。
而如果我们将62.5%转化成分数5/8，那么利用数的整除特性就可以快速来求解。
方法二：原中级以下占总数的1-5/8=3/8，则原中级以下职工人数为3的倍数，排除A、C。又有2名职工评上中级职称后，此时中级以下占总数的1-7/11=4/11，则原中级以下人数减去2是4的倍数，排除D。这样我们就可以快速观察并排除错误选项选择正确答案。
【例2】甲、乙、丙、丁四个工厂共有100名高级技工。其中甲、乙两个工厂的高级技工数量比是12：25，丙工厂的高级技工人数比丁工厂少4人。问丁工厂的高级技工人数比甲工厂（ ）？
A.多6人 B.少6人 C.多9人 D.少9人
【答案】D【解析】方法一：设甲有高级技工12X名，则乙有25X，丙丁之和
通过这两道题同学们可以发现整除简单易上手，能够在一部分题目中帮助我们省去计算的过程快速确定答案，希望同学们勤加练习，在数量关系部分取得更多的分数。
教你学会特值“任意性”题目
“特值法”在解决行测数量关系问题时以其简单的思维和便捷的解题过程深受广大考生的青睐，但对部分考生来说，感觉比较难以掌握。下面对“特值法”进行全面介绍，希望能帮助广大考生快速准确地解决相关问题。
一、什么是特值思想
将题中某个未知量设为特殊值，从而通过简单的运算，得出最终答案的一种思想。这个特殊值应该满足的条件：首先，无论这个量的值是多少，对最终所求结果没有影响；其次，这个量应该要跟最终所求结果有相对紧密的联系；最后，这个量在整个题干中给出的等量关系中是一个不可或缺的量。
二、任意性如何体现
1.题目中概念间存在A×B=M关系：
工程问题、行程问题、浓度问题、其他符合A×B=M关系的问题。
2.题干描述某量为任意性：
数据具有“任意”性：纯字母、无数据，“任意”字眼。
三、如何设特值
接下来我们结合两道例题，来加深大家的理解：
例1.某网店连续3次下调某款手机的零售价格，每次下调幅度分别为：2.7%、5.5%和4.6%。经过3次调价，该款手机零售价较下调前大约下降了：（ ）
A.12.3% B.12.8% C.13.3% D.13.8%
【答案】A【解析】设此款手机的原价为100元，则连续三次下调后手机价格变成100(1%-2.7%)(1%-5.5%)(1%-4.6%)≈87.7元，原价是100，现价是87.7，所以大约下降了12.3%。
另解：第一次下调2.7%后零售价格为初始售价的97.3%，故第二次下调5.5%的降幅要小于初始售价的5.5%，同理，第三次的降幅也小于初始售价的4.6%。2.7%+5.5%+4.6%=12.8%，故总降幅必然小于12.8%，据此排除B，C，D，选A。
例2.如图所示，矩形ABCD的面积为1，E、F、G、H分别为四条边的中点，I是FE上任一动点，问阴影部分的面积为多少（ ）？
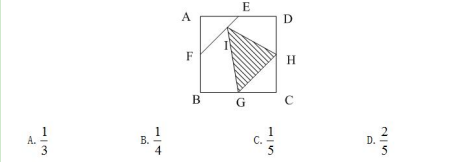
【答案】B【解析】因为I是FE上任一动点，具备任意性，而选项都为确定值，故I点的位置对结果无影响。因此可设动点I到为E点（或F点）。如图所示，此时矩形EDCG占矩形ABCD总面积的一半，而三角形EHG面积又占矩形EDCG面积的一半。矩形ABCD面积为1，故阴影部分面积为1/4。矩形因此选择B选项。
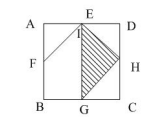
【点拨】在含有任意性的几何题目时，若选项均为定值，我们在设特值时可以结合题目设特殊点（端点、中点）或特殊图形从而简化运算。
特值法用好了可以大幅提升做题速度，但是也不要盲目地什么题都想着特值，一定要理解好特值的思想和应用环境，精准地用好特值！
方程法对行测数量关系有“大作用”
数量关系在行测试卷当中，往往是大家较容易忽略或者说是放弃的。其中原因可能有二：一是自身数学基础薄弱，而数量关系题型复杂广泛，导致产生畏难心理而放弃；二是在相关网站和社交媒体上看到大家都在说数量关系难度较大，没有时间做，从而放弃。其实，我们如果对数量关系稍加研究的话会发现，其实数量关系当中还是有一部分题可以做对，或者是可以很快攻破的。我们会发现这些题会有一个共同的特点：用方程思路解题就会变得简单，所以现在我们就来梳理一些用方程法解决数量关系问题的常见思路。
我们知道用方程法解题的基本思路可以分为四步：
①梳理题干条件，找到等量关系
②把未知量设为未知数
③根据等量关系列式
④求解
下面我们就通过三道例题，感受一下方程法对于解题的帮助：
【例题1】某直播平台对3种农产品进行3小时的直播带货。第1小时，B产品的带货额比A多50万元，C产品只有B产品的60%。第2小时与第1小时相比，A带货额翻倍，B增幅比A少20%，而C增加了两倍。最后1小时共带货3090万元，且A带货额比第1小时增长300%，B、C均比第2小时增长50%。请问第2小时直播带货额为多少（ ）？
A.1580 B.1600 C.1860 D.2000
【答案】C【解析】梳理题干我们会发现“最后1小时共带货3090万元”可作为等量关系列式，但A、B、C的销售额并没有直接给出，需设未知数。但这三小时的销售额之间又有关联，所以我们可以设第1小时B产品销售额为x万元，根据题意，A、B、C三种产品这3小时销售额如下表所示：
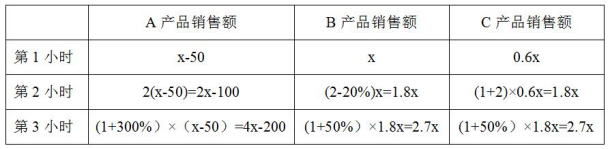
最后1小时(即第3小时)共带货3090万元，则有4x-200+2.7x+2.7x=3090，解得x=350。第2小时直播带货额为2x-100+1.8x+1.8x=5.6x-100=1860万元。选择C项。
【例题2】服装店买进一批童装，按每套获利50%定价卖出这批童装的80%后，按定价的八折将剩下的童装全部卖出，总利润比预期利润减少了390元。问服装店买进这批童装花了多少元（ ）？
A.5500 B.6000 C.6500 D.7000
【答案】C【解析】梳理题干我们会发现“总利润比预期利润减少了390元”可作为等量关系列式，预期总利润-实际总利润=390。可设这批童装成本价为x，数量为10件，梳理题干列表如下：
预期利润为10(1.5x-x)=5x，实际获得利润为4x+0.4x=4.4x，总利润比预期利润减少390元，即5x-4.4x=390，解得x=650。故买进这批童装花了10x=6500元。选择C项。
（注：销量无实际数据，且表示为倍数、分数、百分数形式的，可设销量为特值）
【例题3】小张每天固定时间骑摩托车从家里到乡镇的木材加工厂上班，如果他以30千米/小时的速度行驶，会比上班时间提前10分钟到达加工厂，如果他以20千米/小时的速度行驶，则会迟到12分钟。如果小张某天迟到了6分钟，则他的当天行驶速度是多少千米/小时（ ）？
A.22 B.23 C.24 D.25
【答案】A【解析】梳理题干可得小张以三种不同的速度从家里到工厂，且这三种情况下路程相等。不妨设小张按固定时间出发时，距上班时间t小时，迟到6分钟情况下的行驶速度为v。则有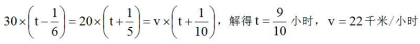
。选择A项。
通过这三道例题，我们可以看出利用方程法解决常见数量关系问题，是十分有效的。所以学好用好方程法对于解题来说是有很大帮助的，大家在学习这一部分内容时一定要引起重视！
