行测数量关系解题技巧汇总
计算问题是行测考试中的常见题型，完全放弃影响分数，直接求解用时较长，接下来政华公考为大家介绍一些简单快速的解题方法。
行测数量关系关键技巧——整除
一、概念
若整数a除以大于0的整数b，商为整数，且余数为0。我们就说a能被b整除（或b能整除a）。在实际做题的过程中，对于概念的考查通常可以判断一下所涉及的量是否符合整数。
二、应用环境
那“整除”具体在什么样的计算问题里应用呢？这就需要大家来了解一下它的应用环境了。
（1）题干出现整除、倍、平均、每等文字表述时。
【例】某生产车间有若干名工人，按每4人一组分，多一个人；按每5人一组分，也多一个人；按每6人一组分，还是多一个，该车间至少有多少名工人？（ ）
A.31 B.41 C.61 D.122
【答案】C【解析】题干描述中出现了“每…人一组”的表述，所以我们可以先来判断一下所求量具备的整除特性。由题意可知，该车间工人数减去1能同时被4、5、6整除，所以结合选项我们不难选出C。
（2）出现分数、百分数、比例等数据时。
【例】林华全家是阅读爱好者，家里有各种书籍，版本也多。已知他家有五分之三的书是中文版的，六分之一是英文版的，八分之一是中英文互译版的，还有多于11本但少于17本是其他版本的。
问：他家有多少本英文版书？（ ）
A.72 B.20 C.15 D.13
【答案】B【解析】题干描述出现分数，优先考虑使用整除特性求解。由题意可知书籍总数×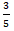
=中文版的数量，书籍总数×
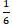=英文版的数量，书籍总数×
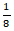=中英文互译版的数量，则林华家书籍总数能同时被5、6、8整除，所以所求的英文版书的数量×6能被5、8整除，即选项×6能被5、8整除，选B选项。
三、例题演练
接下来通过一道例题来感受下“整除”的魅力吧。
【例】某镇政府办公室集中采购一批打印纸，分发给各个职能部门。如果按每个部门4包分发，则多6包；如果按每个部门5包分发，则有1个部门只能分到3包。这批打印纸的数量是：（ ）
A.38包 B.36包 C.40包 D.42包
【答案】A【解析】常规思路：假设有x个部门，则根据打印纸总量不变可得方程：4x+6=5x-2，解得x=8，所以打印纸的总数=5×8-2=38包，选A选项。
利用整除解题：题目出现了“每……”的表述，所以根据题意可知打印纸的总数满足两个条件：①总数减掉6之后，可被4整除；②总数+2之后，可被5整除。所以选A选项。
行测数量关系关键技巧——尾数法
一、应用环境
其实很多考生都会有一个误解，加减运算这不是小学时候学习的吗？这我难道还不会吗？其实加减法计算对于大家来说可能真没有问题，但是如何快速而且精算计算出结果，就有问题了，比如看下面这道题：
【例】379+265+344=？（ ）
A.976 B.877 C.988 D.989
【答案】C【解析】相信这道题真让大家选出答案来也没问题，但是能不能快速而且口算就得出结果呢？相信还是有难度的，其实在这里啊，可以去观察选项，大家有没有发现，选项的末一位都是不相同的，在这里我们就可以利用这个不同去解决这个问题。我们都知道加减法运算都是从尾数开始计算的，所以我们只需要根据选项的尾数不同去计算就可以了。这道题，三个数的尾数：9+5+4=X8。答案直接就可以选择C选项了。这种方法是不是既精确又快速呀。
二、关键要点
1.选项尾几位不同计算加减几位。
在进行加减精准运算的时候，一定要先注意观察选项尾几位不同，选项尾几位不同就加减几位，千万不要直接去加减一位，比如看下面的例题：
【例】376.26+477.23+334.88+127.44=？（ ）
A.1234.61 B.1315.81 C.1324.11 D.1312.91
【答案】B【解析】我们来看到这道题，很显然所有数字的尾数都是1，如果我们直接去加尾一位，那么将无法选择结果。此时我们就需要及时观察选项，很显然选项是尾两位不同，所以数字就可以直接加尾两位——26+23+88+44=X81。此时我们就可以选择答案：B。
2.计算过程一定要注意数位对齐。
这里主要指的是，我们在遇到有小数点的数字加减的时候，一定要注意小数点后面的数字数位是否一致，我们经常会因为不注意数位的不对齐而计算错误，比如：
【例】276.33+311.6+119.61+96.7+112.66=？（ ）
A.916.34 B.917.23 C.918.91 D.916.90
【答案】D【解析】这一道题是考试当中非常容易错的题目，很多考生看到题目发现是简单加减运算，然后一观察，选项的尾一位不相同，所以直接加尾一位：3+6+1+7+6=X3。毫不犹豫选择了B选项。其实这么做错了，大家仔细观察一下，311.6、96.7这两个数字是小数点后面只有一位，而选项的数字都是小数点后面尾两位。所以此时我们一定要注意这个地方的数位是不相同的，政华公考建议大家可以采用补“0”法，指的就是将这些小数点后面少了一位的数字后面补上一个0，这样就不会出错了。所以这道题很显然尾数就变成了：3+0+1+0+6=X0。结果选择D选项。
3.加减混合运算，采用先加后减。
这里指的是，有时候我们在计算过程中，会遇到加减混合运算的题目，此时为了避免出错。我们可以将加法的尾数先加起来，减法的尾数再加起来，最后再做减法，这样一般出错概率会非常低。
【例】347+469-344-371+273-366+273=？（ ）
A.281 B.273 C.288 D.269
【答案】A【解析】我们观察可以看到，选项都是尾一位不同，但此时计算里面加减运算都有，一旦符号弄错，就会计算错误。所以我们这里建议先把加法数字的尾一位加起来：7+9+3+3=X2，再把减法数字的尾一位加起来：4+1+4=X1。最后直接把加法数字尾一位减去减法数字尾一位：2-1=1。结果直接选择A选项。
行测数量关系关键技巧——赋值法
一、题型特征
1）题干含中有A=B×C的形式。
2）题干中有分数、百分数、比例、倍数等。
二、常用题型
工程问题、行程问题、溶液问题、经济利润问题。
三、赋值原则
1.A=B×C中：
优先赋值总量A（一般A为不变量）；赋成B或C的公倍数。A变化，则赋值B或C（存在比例关系优先）；B或C按比例赋值。
2.A=B×C中，无具体值，仅有比例关系，赋值两次。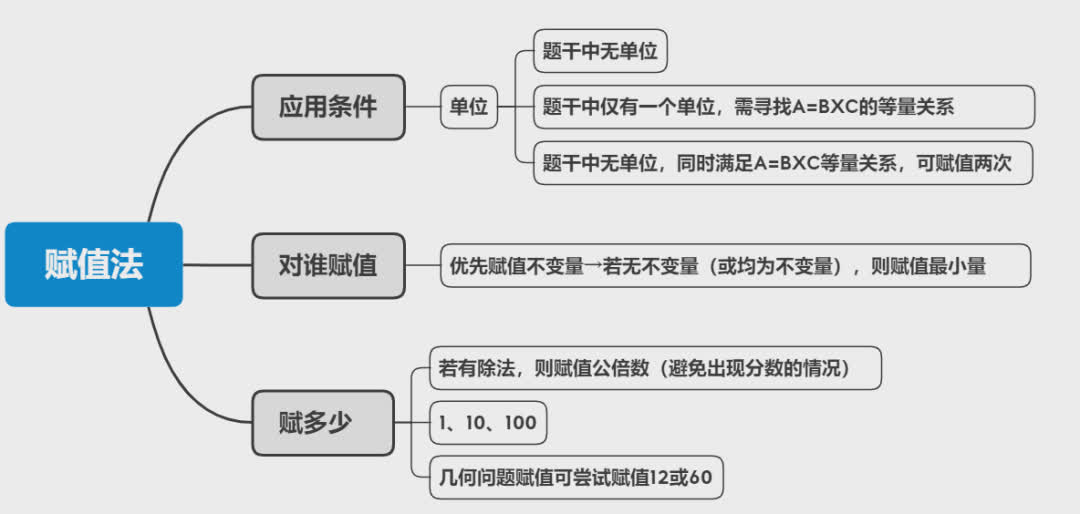 
四、知识应用
【例】（2019联考）某楼盘的地下停车位，第一次开盘时平均价格为15万元/个；第二次开盘时，车位的销售量增加了一倍、销售额增加了60%。那么，第二次开盘的车位平均价格为：（ ）
A. 10万元/个 B. 11万元/个
C. 12万元/个 D. 13万元/个
【答案】C【解析】第一步，本题考查基础公式类经济利润问题，用赋值法解题。第二步，销售额=平均价格×销售量，已知第一次开盘平均价格为15万元/个，赋销售量为1，则销售额为15万。第二次开盘时，销售量增加了一倍，即为2，销售额增加了60%，得销售额为15×（1+60%）=24（万元），故第二次开盘平均价格为24÷2=12（万元/个）。因此，选择C选项。
【例】（2014四川）某钢厂生产一种特种钢材，由于原材料价格上涨，今年这种特种钢材的成本比去年上升了20%。为了推销该种钢材，钢铁厂仍然以去年的价格出售，这种钢材每吨的盈利下降40%，不过销量比去年增加80%，那么今年生产该种钢材的总盈利比去年增加了多少？（ ）
A. 4% B. 8% C. 20% D. 54%
【答案】B【解析】第一步，本题考查经济利润问题，属于利润率折扣类，用赋值法解题。第二步，总利润=单利润×销量，根据“盈利下降40%”，赋值去年每吨利润为10，可得今年每吨盈利为10×（1-40%）=6；根据“销售量比去年增加了80%”，赋值去年销售量为10，可得今年销售量10×（1+80%）=18，故去年总盈利为10×10=100，年总盈利为6×18=108。第三步，今年总盈利比去年增加（108-100）/100=8%。因此，选择B选项。
【例】（2019联考）2016年某电子产品定价为n元/台，2017年由于技术升级成本降低，定价降低10%。每台产品利润提升10%，2017年全年销售这种产品的总利润较2016年增加了21%，2017年的销量比2016年：（ ）
A.提升了不到20% B. 提升了20%或以上
C. 降低了不到20% D. 降低了20%或以上
【答案】A【解析】第一步，本题考查经济利润问题，用赋值法解题。第二步，总利润=单利润×销量，赋值2016年利润为10，销量为10。根据“每台产品利润提升10%”，可得2017年每台产品利润为10×（1+10%）=11；根据“2017年全年销售这种产品的总利润较2016年增加了21%”，2016年总利润=10×10=100，则2017年总利润=100×（1+21%）=121，根据总利润=单利润×销量，可得2017年销量=121÷11=11。第三步，2017年的销量比2016年增加（11-10）/10=10%。因此，选择A选项。
通过比较发现，数量关系的这几类技巧方法可以辅助我们更加直接的选出正确选项，一定程度上精简了计算过程，可谓事半功倍。大家快快练起来吧！
