政华公考

一副完整的扑克牌，共54张，包括大王、小王、四种花色的牌各13张，题干要求保证6张牌花色相同，利用最不利原则，尽可能让保证的6张花色相同不出现，即已经抽出某种花色的牌5张，去抽取该花色第6张牌时，未能发生，取到了其它花色，如此操作，我们可先抽出四种花色的牌各5张，又将大、小王抽出，此时再任意抽取一张，就会出现题干要求的情况，因此最不利情况数为4×5+1+1=22张，根据“所求的保证数=最不利的情况数+1”可得，所求为22+1=23张。

以上就是最不利原则所解题目的题型特征和解题思路，下面请大家练习使用最不利原则解题。

1.某会展中心布置会场，从花卉市场购买郁金香、月季花、牡丹花三种花卉各20盆，每盆均用纸箱打包好装车运送至会展中心，再由工人搬运至布展区。问至少要搬出多少盆花卉才能保证搬出的鲜花中一定有郁金香？（）

A.20盆 B.21盆 C.40盆 D.41盆

【答案】D【解析】题干出现“至少……才能保证”，可考虑利用最不利原则解题。考虑最不利情况，将月季花和牡丹花全部搬出，此时再搬出一盆即可满足条件，即至少需要搬出20+20+1=41盆。故本题选D。

2.某大学有240名学生参加冬奥会志愿者选拔活动，他们均来自文学院、外学院、信息管理学院和经济学院四个学院，分别有85、60、55和40人。问：至少有多少人选拔成功，才能保证一定有50个选拔成功的学生是专业相同的？（）

A.188 B.198 C.180 D.201

【答案】A【解析】题干出现“至少……才能保证”，可考虑利用最不利原则解题。考虑最不利的情况，先将经济学院40人选出，其他学院的各选拔49人，此时再多选1人，即可保证一定有50个选拔成功的学生是专业相同的，即至少有40+49×3+1=188人选拔成功。故本题选A。

3.某单位组织党员参加党史、党风廉政建设、科学发展观和业务能力四项培训，要求每名党员参加且只参加其中的两项。无论如何安排，都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员？（）

A.17 B.21 C.25 D.29

【答案】C【解析】题干中未直接出现“至少……才能保证”，但分析题意，最后一段可转化为，该单位至少有多少党员，无论如何安排，都能保证至少5名党员参加的培训完全相同，因此此题仍然符合最不利原则的题目题型特征。先考虑培训的种类数，每名党员从四项培训中选两项参加，共有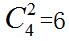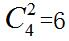种选法。再考虑最不利的情况，每种选法有4人选择，此时再来1人选择，即可满足至少5名党员参加的培训完全相同，即该单位至少有4×6+1=25名党员。故本题选C。

政华公考希望通过上面例题的学习，能够让同学们对最不利原则问题的特征和解法有更多的了解，对大家备战数量关系有所帮助。

奇偶数的神奇运用

行测考试中数量关系一直令很多考生望而生畏，考生对题目不熟悉，解题耗时长且易出错。出现这样问题关键在于各位考生对于一些基础的数学知识早已遗忘，因此掌握数论知识对攻克数量关系非常有必要的，下面政华公考带大家来学习数论知识——奇偶数。

一、概念

奇数：不能被2整除的整数称为奇数；

偶数：能被2整除的整数称为偶数。

二、运算性质

性质1：

偶数±偶数=偶数，奇数±奇数=偶数，奇数±偶数=奇数。

例：16和12均为偶数，16+12=28、16-12=4，结果均为偶数。

15和13均为奇数，15+13=28、15-13=2，结果均为偶数。

17和16一奇一偶，17+16=33、17-16=1，结果均为奇数。

性质2：

偶数×奇数=偶数，偶数×偶数=偶数，奇数×奇数=奇数。

例：13和6一奇一偶，13×6=78，结果为偶数。

16和2均为偶数，16×2=32，结果为偶数。

15和3均为奇数，15×3=45，结果为奇数。

推论1：若几个整数的和（差）为奇数，则这些数中奇数的个数为奇数；若为偶数，则这些数中奇数的个数为偶数。

例：1+2+3+4+5+6+7+8+9=45，结果为奇数，其中奇数有5个，为奇数个。

1+2+3+4+5+6+7+8=36，结果为偶数，其中奇数有4个，为偶数个。

推论2：如果几个整数的乘积是奇数，那么这几个数均为奇数；

如果几个整数的乘积为偶数，那么这几个数中至少一个偶数。

例：1×3×5×7×9=945，结果为奇数，乘数全为奇数。

1×2×3×5×7×9=1890，1×2×3×4×5×7×9=7560……，结果为偶数，乘数中至少有一个偶数。

推论3：两数之和与两数之差奇偶性相同。

例：23+21=44，为偶数；23-21=2，也为偶数。35+32=67，为奇数，35-32=3，也为奇数。

三、应用

（一）解不定方程

例1：办公室工作人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可以装7份文件，每个蓝色文件袋可以装4份文件。要使每个文件袋都恰好装满，需要红色、蓝色文件袋的数量分别为（）个。

A.1、6 B.2、4 C.4、1 D.3、2

【答案】D【解析】设红色文件袋x个，蓝色y个，依据题意得，7x+4y=29，4y为偶数，29为奇数，则7x为奇数，即x为奇数，排除B、C。代入A项，7×1+4×6=31，不符合，排除A，直接选择D。

（二）奇偶性判断

例2：某班部分学生参加数学竞赛，每张试卷有50道试题。评分标准是：答对一道给3分，不答的题每道给1分，答错一题扣1分。问：这部分学生得分总和是奇数还是偶数？（）

A.奇数 B.偶数 C.都有可能 D.无法判断

【答案】B【解析】因为不知道学生人数，所以求出总得分是不可能的，那我们从每个学生的得分入手。因为每道题目无论答对、答错或者不答得分都是奇数，所以50道题目得分是50个奇数相加为偶数，则每个人总得分为偶数。因为任意个偶数相加结果都为偶数，所以学生分数总和为偶数。选择B选项。

（三）已知两数之和（差），求两数之差（和）

例3：一个人到书店买了一本书和一本杂志，在付钱时，他把书的定价中的个位数和十位数看反了，准备付21元取货。售货员说，“你应该付39元才对”。请问书比杂志贵多少元？（）

A.20 B.21 C.23 D.24

【答案】C【解析】书和杂志价钱之和为39元，根据推论“两数之和与两数之差奇偶性相同”，可得书和杂志的差为奇数，排除A、D选项。代入C，计算可得书为31元，杂志为8元。书的定价个位数和十位数颠倒后，总价为13+8=21元，符合题意，则选择C选项。

熟练应用奇偶数的运算性质及推论，可以巧妙地解决数量关系的部分题目，政华公考希望各位考生能够多加练习，掌握这类题目。

巧用特值法解决利润问题

利润问题是行测数量关系考试中的常见考点，部分考生觉得这类题型题干信息和条件多，做起来比较慢。如果我们能够掌握一定的方法和技巧，将有助于我们解题。在此政华公考给大家介绍一下如何巧用特值法解决利润问题。

【例1】某家具店购进一批桌椅，每套进价200元，按期望获利50%定价出售。卖掉这批桌椅的60%以后，店主为提前收回资金，打折出售余下的桌椅。售完全部桌椅后，实际利润比期望利润低了18%。问余下的桌椅是打几折出售的？（）

A.七五折 B.八二折 C.八五折 D.九五折

【答案】C【解析】本题中桌椅的销量无实际值，而是以百分数的形式给出相关条件，不妨设这批桌椅的总量为10，打折后出售的价格为x。由题意，整理相关信息如下：

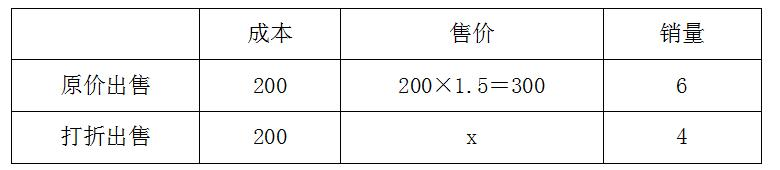
根据实际利润比期望利润低了18%，有（300-200）×6+4（x-200）=（300-200）×10×（1-18%），解得x=255。因此打折后出售的价格为255元，255÷300=0.85，即余下的桌椅是打八五折出售的，故本题选C。

【例2】一批货物，本来按获得50%的利润来定价。结果只卖出70%的货物，为尽早卖出余下的货物，商店决定按定价打折销售，这样所获得的全部利润，是原来的期望利润的82%，问打了多少折？（）

A.2.5折 B.5折 C.8折 D.9折

【答案】C【解析】本题没有给我们关于价格和销量具体的数值，只以百分数的形式给出相关条件，我们不妨设货物的成本价为100，这批货物的总量为10，打折后出售的价格为x，由题意，整理相关信息如下：

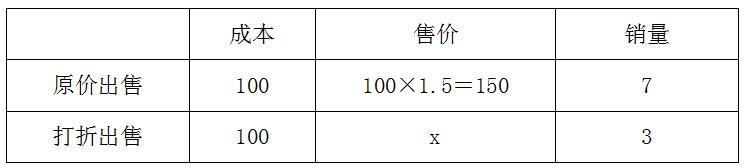
根据所获得的全部利润是原来所期望利润的82%，有（150-100）×7+（x-100）×3=（150-100）×10×82%，解得x=120。因此打折后的售价为120元，120÷150=0.8，即打了8折，故本题选C。

思路点拨：在利润问题中，通常会涉及成本、售价、销量、利润、利润率和折扣这些基本概念。如果条件比较复杂，可以通过列表梳理各个概念间的关系。同时，我们还可以结合特值法简化计算过程：

1.价格无实际数值，且价格间关系表示为倍数、分数或百分数形式，可设成本或售价为特值；

2.销量无实际数值，且销量间关系表示为倍数、分数或百分数形式，可设销量为特值。

最后，政华公考提醒各位考生，平时做题时多多总结，以提高对利润问题的概念以及如何设特值的敏感性。