
行测数量关系:如何快速掌握和定最值问题
巧解和定最值问题
在行测考试当中,数量关系往往是最容易被同学们放弃的部分,有些同学一看到数量的题目下意识的就想放弃,其实这种想法是不可取的,数量的题目当中也存在一些易得分的题型,就比如说和定最值问题,今天就来说一说如何解决这类问题。
一、题型特征
已知多个数的和一定,求其中某数最值的问题。
二、解题原则及方法
求某个量的最大值,其他量应尽可能小。
求某个量的最小值,其他量应尽可能大。
三、习题练习
例题1:一次数学考试满分为100分,某班前六名同学的平均分为95分,排名第六的同学得86分,假如每个人得分是互不相同的整数,那么排名第三的同学最少得多少分( )?
A.94 B.97 C.95 D.96
【答案】D【解析】要使排名第三的同学得分最少,则应使其他同学得分尽量多,前两名同学最多分别得100分和99分。设排名第三的同学最少得x分,则排名第四、五名的同学最多分别得x-1,x-2分,有100+99+x+(x-1)+(x-2)+86=95×6,解得x=96,故排名第三的同学最少得96分。
规律总结:根据解题原则确定不了具体量的值,可以设未知数列方程求解。
例题2:六一儿童节期间,100名幼儿园学生参加5项活动,参加人数最多的活动人数不超过参加人数最少活动人数的2倍,则参加人数最少的活动最少有多少人参加( )?
A.10 B.11 C.12 D.13
【答案】C【解析】设参加人数最少的活动有x人,则参加人数最多的活动人数为2x人,要想参加人数最少的活动人数最少,则参加其他项目的人要尽可能多,那么参加其他三项活动的人数也可均为2x,则有2x×4+x=100,解得x=11.X,向上取整可得x=12,故参加人数最少的活动最少有12人参加。
规律总结:根据方程求解时,求出的数不是整数,问最小(至少),向上取整。
例题3:植树节来临之际,120人参加义务植树活动,共分成人数不等且每组不少于10人的六个小组,每人只能参加一个小组,则参加人数第二多的小组最多有( )人。
A.32 B.34 C.36 D.38
【答案】C【解析】和一定,要使第二多的小组的人数尽量多,则其他小组的人数应尽可能少,设参加人数第二多的小组有x人,如下:

则有(x+1)+x+13+12+11+10=120,解得x=36.5,因所求为整数,且为最多,故向下取整,即参加人数第二多的小组的人数最多有36人。
规律总结:根据方程求解时,求出的数不是整数,问最多(最大),向下取整。
通过以上几道题目,相信同学们已经对和定最值问题有了一定的了解,希望大家可以快速的掌握这种题型的解题方法,让这类题目不再成为我们学习路上的阻碍。
行测和定最值问题之三步解题
首先,我们得知道怎样的题型是属于和定最值问题!和定最值,此类题型的特点就是一组数的和是一个定值,要我们求其中某个量的最大(小)值。例如,一个班上6名同学的总分和为490分,问最高分同学得分最低得几分?这就是一种典型的和定最值问题,对于这种题目,我们只需要进行下列三个步骤即可快速求解:
1.对未知数由大到小排序:一、二、三……
2.标箭头:↓↑(求某个量最大(小),则其余量尽可能小(大))
3.设所求为x,结合条件把其它量表示出来,再根据和一定构建等量求解。
例1:5人参加百分制考试,成绩总和为330分,已知5人都及格了,成绩均为整数且依据成绩排名无并列名次,求第一名最少得了多少分( )?
A.67 B.68 C.69 D.70
【答案】B【解析】5个得分为5个数,和一定,求第一名的得分最小值,典型和定最值问题,直接三步走:
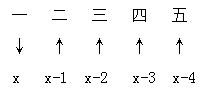
第一步:写一~五,由大到小排序;第二步:“一”要最小,标个“↓”,那么在和一定的情况下,其他量都要大,标“↑”;第三步:设“一”为x,由于“一”求最小“二”尽可能大,两个数需要尽可能接近且均为整数,故差1满足,依次类推得到其余数的取值。根据得分总和为330构建等量关系:5x-10=330,解的:x=68,答案选B。
例2:植树节来临之际,120人参加义务植树活动,共分成人数不等每组不少于10人的六个小组,每人只能参加一个小组,则参加人数第二多的小组最多有多少人( )?
A.32 B.34 C.36 D.38
【答案】C【解析】6个小组的人数为6个数,他们和为120,是个定值,和定最值问题,直接三步走:
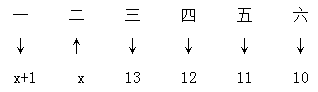
由大到小排序后,“二”要大,其余要小,标相应的箭头;设“二”为x,那么“一”要小但又不相等,所以为x+1,又“三、四、五、六”依次要小,且最小不少于10,又互不相等,所以依次为13、12、11、10,根据6个数的和构建等量关系:2x+47=120,解得:x=36.5,求出来的x为最大值,也就是说x≤36.5,同时又是整数,故所求为36,答案选C。
此类方法其实就是准确按照三个步骤去解题即可。接下来在备考过程中勤加练习,准确判断题目是否符合和定最值的题型,进而用此方法快速解决问题。
两招解决和定最值问题
由于行测数学运算涉及的知识点较多,一直以来是各位考生比较头痛的部分,尤其是遇到考查极限思维的极值类问题,大部分考生选择直接放弃做这类题目。其实极值类问题中有一种题型相对简单,只要掌握一定的解题技巧就可以轻松应对的和定最值问题。
【题干特征】
若干个量的加和是定值,且求某量的最大值或者最小值。
示例:两个正整数的和为15,求①最大的数最大是多少?②最大的数最小是多少?
解析:①要求最大的数最大,另一个数要尽可能小,最小为1,最大的数最大为14;②要求最大的数最小,另一个数要尽可能大,再大也不能比最大的数大,最大为7,故最大的数最小为8。
【解题原则】
1.和一定时,求某量的最大值,让其他量都尽量小。
2.和一定时,求某量的最小值,让其他量都尽量大。
【刷题巩固】
【例1】七个小朋友共采摘草莓43颗,且每人采摘的数量互不相等,采摘草莓数量最多的小朋友最多采摘了( )颗。
A.20 B.21 C.22 D.23
【答案】C【解析】七个小朋友采摘的草莓数量和一定,要使数量最多的小朋友采摘的草莓数量最多,应让其他小朋友采摘的尽量少,又由于每个小朋友采摘数量互不相等,故其他六个小朋友采摘的数量从小到大依次是1、2、3、4、5、6,则数量最多的小朋友最多采摘43-6-5-4-3-2-1=22颗,故选C。
【例2】五人的体重之和是423斤,他们的体重都是整数,并且各不相同,则体重最轻的人最重可能为( )。
A.80斤 B.82斤 C.84斤 D.86斤
【答案】B【解析】五人的体重之和是423斤,想求体重最轻的最重,则需要其他人的体重尽可能轻且为各不相同的整数,若设体重最轻的人最重x斤,则其他四人体重从轻到重依次为(x+1)、(x+2)、(x+3)、(x+4)斤,根据和为423斤,列方程有x+x+1+x+2+x+3+x+4=423,解得x=82.6,体重最轻的人最重为82.6斤,不能比82.6斤再重,因此向下取整最重为82斤,故选B。
“小系数,同方向”解行测和定最值
应用前提
这类题目既然属于和定最值问题,那么必然满足和定最值的条件:和定、求最值。也就是题干中直接或间接给出了几个数“和一定”的描述,让求最大值或最小值。除此之外,还需能根据题干条件列出不确定具体系数的二元一次方程组。此时,我们只需要依据题干信息确定系数即可,具体为“小系数,同方向”。
口诀含义
小系数,即从系数较小的未知量入手;同方向,小系数与自身未知量取值方向相同,大系数与小系数方向相同。
经典例题
例1:观众对五位歌手的歌曲进行投票,每张选票都可以选择五首歌曲中的一首或多首,但只有选择不超过3首歌曲的选票才是有效票。五首歌曲的得票数分别为总票数的82%、73%、69%、51%和45%,那么本次投票的有效率最高可能为:( )
A.95% B.90% C.85% D.80%
【答案】B【解析】根据题干信息,可假设本次参与投票的观众共100人,则这100名观众共投出82+73+69+51+45=320票。设有效投票的人数有x人,无效投票的人数有y人,则有x+y=100;每首歌曲可投的票数有1、2、3、4、5票,不超过3票为有效票,可得n1x+n2y=320(其中n1=1、2、3,n2=4、5),根据“小系数,同方向”可知,x前的系数较小,优先看x前系数,要使投票有效率尽可能高,则有效投票尽可能多,即x前系数要尽可能大,那么y前的系数也要尽可能地大,此时n1=3、n2=5,则有3x+5y=320,联立方程解得x=90,即本次投票的有效率最高为90÷100×100%=90%,选择B。
例2:参加某部门招聘考试的共有120人,考试内容共有6道题。1至6道题分别有86人、88人、92人、76人、72人和70人答对,如果答对3道或3道题以上的人员能通过考试,那么至少有多少人能通过考试( )?
A.32 B.40 C.50 D.61
【答案】D【解析】根据题干信息,本次考试共答对86+88+92+76+72+70=484题,设本次考试通过的有x人,没有通过的有y人,根据共120人参加考试,可得x+y=120,共答对484题,可得n1x+n2y=484(其中n1=3、4、5、6,n2=1、2),根据“小系数,同方向”可知,y前的系数较小,优先看y前系数,要使通过考试的人最少,则未通过考试的人答对的题目尽可能多,即y前系数要尽可能大,那么x前的系数也要尽可能地大,此时n1=6、n2=2,则有6x+2y=484,联立方程解得x=61,选择D。
通过以上题目,我们可以看到解决这类和定最值问题,关键是理解“小系数,同方向”这一解题原则,大家可以多找一些此类题目练习,以便熟练地掌握此种方法。








