简单加减问题
简单加减问题快来复习一下：
题型特征：
一般问题涉及xx和xx共多少，相差多少，或者xx比xx多多少/少多少？
且问题中每个主体的数据在材料中都能直接找到
基本方法：
加减运算、尾数法、截位法
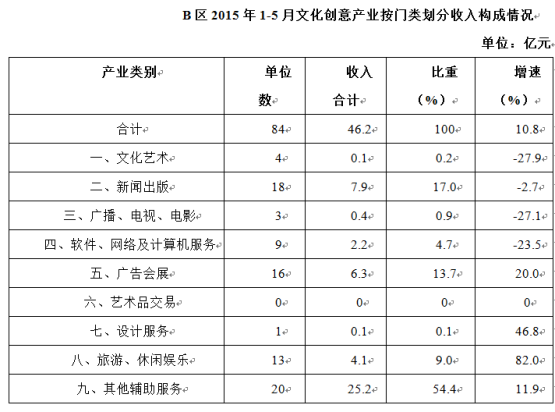
例（2016北京）文化创意产业九大领域中，2015年1—5月收入增速最快的三个领域共有多少家单位（ ）。
A.16 B.30 C.39 D.54
思路梳理
根据表格中的增速确定出排名前三的领域分别是哪些，然后再将单位数加和即可。
解题步骤
从表格中可以看出，2015年1-5月收入增速最快的三个领域为旅游、休闲娱乐、设计服务和广告会展。三个领域共有13+1+16=30家。
故正确答案为B。
间隔增长率的常见考法
间隔增长率特指中间间隔一年的增长率，在近年的国考、省考中考的比较多，而且变形多种多样。值得考生花费时间学习，容易上手，计算量不大。
公式介绍：R=R1+R2+R1*R2
比如2017年比2015年增长了多少（%）？、指2017年和2016年的增长率。
间隔增长率
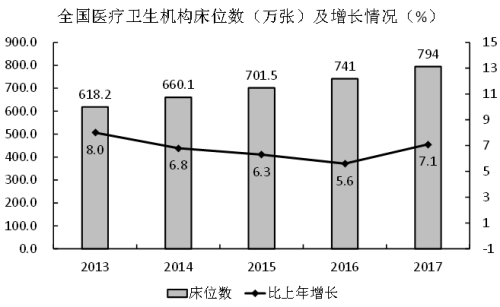
例题
（2019山东）虽然2014-2016年间全国医疗卫生机构床位数增长速度持续下滑，但2016年床位数仍然比2014年增加了：
A.12.26% B.10.87% C.12.31% D.9.69%
【解析】判定题型，2016年比2014年增长了（%），判定为间隔增长率R1=5.6%。R2=6.3%。根据间隔增长率的计算公式：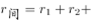
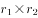，可得全国医疗卫生机构2016年相较于2014年增长率为5.6%+6.3%+5.6%*6.3%≈11.9%+0.35%=12.25%，最接近A选项。故正确答案为A。
间隔基期量
例题
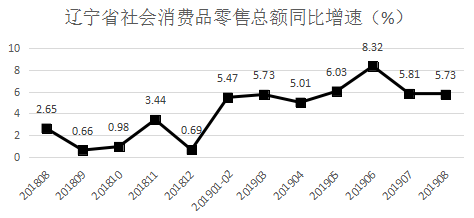
（2019辽宁）2017年8月，辽宁省社会消费品零售总额约为：
A.1121亿元 B.1184亿元 C.4750亿元 D.8633亿元
【解析】判定题型，题目中给2018和2019年数据，问2017年的量，判定题型为间隔基期量。基期量=现期量/1+r，这里增长率为间隔增长率，r1=5.73%，r2=2.65%,根据间隔增长率公式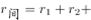
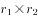=2.65%+5.73%+2.65%*5.73%≈2.65%+5.73%=8.38%。定位表格材料可知2019年8月，辽宁省社会消费品零售总额为1280.7亿元，根据基期计算公式可计算得2017年8月辽宁省社会消费品零售总额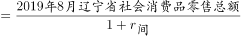
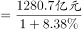
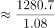
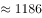亿元，与B项接近。
故正确答案为B。
间隔倍数
例题
与上年同期相比，2015年7月京津冀区域13个城市平均PM2.5和PM10浓度分别上升和。
（2018浙江B）关于2015年7月空气质量状况，能够从上述资料中推出的是：
C.如保持当月同比增速，2017年7月京津冀区域PM2.5浓度将超过2015年7月的两倍
【解析】：判定题型，2017年7月超过2015年7月的多少倍，判定为间隔倍数。根据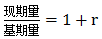
，这里增长率为间隔增长率
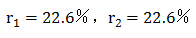。间隔增速为
。
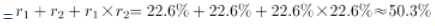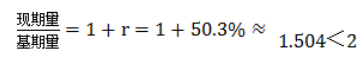。错误。
间隔增长率的四种考法看似很难，其实从时间上进行判定就简单了很多，无论是间隔增长率、间隔基期量、还是间隔倍数，中间都是间隔了一年；做法都是先计算出间隔增长率，然后再代入对应的基期、增长量和倍数公式即可。
增长量的常见问法你知道吗？
题型特征：
常见问法为“增长最多/少的是……”
基本公式：
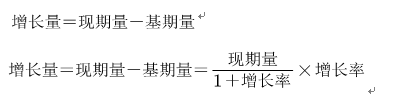
比较方法：在考场上为了提升做题速度，在比较增长量大小时，一般可以直接比较现期量与增长率的乘积。
2013年1—9月，苏南、苏中、苏北地区规模以上工业增加值为11762.9亿元、4900.9亿元、4829.0亿元，同比分别增长9.2%、13.1%、14.5%，苏北增幅比全省平均高3.0个百分点，沿海地区规模以上工业增加值3652.9亿元，同比增长14.2%，增幅比全省平均高2.7个百分点。
例题：2013年1—9月，江苏省规模以上工业增加值同比增加量最多的地区是（ ）。
A.苏南地区 B.苏中地区 C.苏北地区 D.沿海地区
思路梳理
题干出现“同比增长量最多的地区是”可知本题为增长量的比较问题。定位文字材料给出现期量和增长率，利用公式
去比较求解。
解题步骤
定位文字材料可知，本题四个地区的增长率相差不多，根据公式
，增长率相近时，增长量大小主要取决于现期量，苏南地区的现期量远远大于其他地区，因此苏南地区的增长率最多。
故正确答案为A。
怎么分清到底增长了几次
在做资料分析的时候，大家在面对一类题型的时候往往是比较头疼的，这类题型就是与年均增长相关的题型。那么怎么来找到正确的初期末期，下面为大家解析：
第一种题型：直接给出时间段的题型。
什么叫做直接给出时间段型呢？顾名思义，就是题目直接告诉我们两个年份，中间夹着一段时间，求年均增长的问题。对于这种题型，那么直接给出的两份就分别是初期和末期，增长次数可以直接通过两个年份的数值作差来求得。
举个例子来说明一下：
【例1】2011-2016年，我国入境游客中外国游客平均每年增长多少万人次？
【解析】对于这种问题，因为前面给了我们2011和2016这两个年份，所以初期就是2011年，末期就是2016年，那么增长次数就是两个年份的数值直接作差，2016-2011=5，为5次。
第二种题型，间接给出时间段的题型。
那么什么叫间接呢，大家比较常见的就是类似“十一五时期”，“十二五时期”这种用语言来描述的情况，咱们就可以理解为是间接给出的。那么对于这种题型首先咱们得先清楚概念性指标所描述的时间具体指的是哪段，比如“十一五时期”指的是2006-2010年，“十二五时期”指的是2011-2015年。
在分析初期末期是哪年之前，先来讨论一个概念。咱们可以把资料分析中遇到的数据，根据性质分成两种，一种是时间段上的数据，咱们可以理解为可累计的数据，另一种是时间点上的数据，不可累计的数据。时间段上的数据，比如2011年全年的出生人数，死亡人数，总收入，净利润，等等;时间点上的数据，比如2011年末的全国总人口数，规模以上企业数量，美元对人民币的汇率，等。
对于时间段上的数据而言，“十二五时期”内的平均每年，那么就是共计5个完整的年份，每份都是一年这个时间段，所以初期就是2011年，末期就是2015年，增长次数是4。
对于时间点上的数据而言，“十二五时期”应该是从2011年的年初至2015年的年末，但是年末与年初之比不叫做同比，而2011年的年初换言之就应该是2010年的年末，所以说到这里，大家可能就知道了，这种情况之下我们就要把初期变成2010年年末，而末期依然是2015年年末，增长次数也随之变成了5才对。
举两个例子来说明一下：
【例2】“十二五时期”内全国人口数量的年平均增长量是多少？
【解析】由于全国人口数量，属于时间点上，不可累计的数据，所以若材料当中给的各年份年末的人口数，则初期为2010年末，末期为2015年末，增长次数为5次。
【例3】“十二五时期”内出生人数平均每年增长百分之多少？
【解析】由于年内出生人数属于累计数据，时间段上的数据，所以材料中一般会给我当年全年的累计数据，那么初级就是2011年，末期就是2015年，增长次数为4。
