
行程问题属于行测的常考题型,在行程问题当中,我们固有的思维都是应用方程法来解题,那其实还有一个更加简单的方法,就是正反比。应用正反比来解题,可以提升我们的做题速度,那接下来带大家一起学习一下如何应用正反比来解行程问题。
我们知道在行程问题当中,基本公式S=VT。
公式中满足以下比例关系:
1、路程一定时,速度与时间成反比
2、速度一定时,路程与时间成正比
3、时间一定时,路程与速度成正比
总结:两个量相乘为定值,这两个量成反比;两个量相除为定值,这两个量成正比。
应用环境:存在M=A×B的关系,且存在不变量。
我们在考察过程中一般都是会给到其中的一个量为定值,根据另外两个量所成的正比或反比关系求出比例关系,进而根据比例关系求出实际量。
例题1:
经技术改进,A、B两城间列车的运行速度由150千米/小时提升到250千米/小时,行车时间因此缩短了48分钟,则A、B两城间的距离为:
A.300千米 B.291千米 C.310千米 D.320千米
【解析】答案:A。A、B两城间的距离没有发生变化,即路程一定,我们已知s=vt,两数相乘为定值,因此,速度和时间成反比的关系,提速前后速度之比为150:250,即3:5,则时间之比为5:3,由题干信息可得,时间缩短了48分钟,由时间关系可知,现在的时间比原来的时间少2份,2份对应48分钟,因此1份时间对应24分钟,原来时间为5份,即为24×5=120分钟=2小时。所求路程=速度×时间=150×2=300千米,选择A选项。
例题2:
一战斗机从甲机场匀速开往乙机场,如果速度提高25%,可比原定时间提前12分钟到达;如果以原定速度飞行600千米后,再将速度提高1/3,可以提前5分钟到达。那么甲乙两机场的距离是多少千米?
A.750 B.800 C.900 D.1000
【解析】答案:C。从甲机场到乙机场,路程一定,速度与时间成反比,第一次提速前后速度比4:5,则时间比为5:4,差了一份,相差12分钟,则原速走完全程需要5份,也就5×12=60分钟。第二次提速前后速度比为3:4,则时间比为4:3,差5分钟,即原来的速度走完后面的路程需要4份时间,也就是4×5=20分钟;可得原速走600千米需要60-20=40分钟,则原速为600千米÷40分钟=15千米/分钟,则全程为15千米/分钟×60分钟=900千米,故选择C选项。
通过以上两道例题,我们会发现,当行程问题中存在不变量时,如果我们能有效地利用正反比来进行解题的话,很多复杂的题目就变得清晰明朗,大家多去练习一下。
植树问题怎么解决
数量关系题目在行测考试中每道题所占的分值较大,放弃十分可惜,但因为题目难度较大,题型多变,涉及知识点较广等原因,使得很多考生产生了望而却步的心理状态。这样心理状态的产生,其实是考生对于一些知识点掌握不够扎实,也有可能是对于一些不常出现的题型,没有进行系统的总结和学习。而植树问题也是其中一种题型,只要掌握题干特征和做题方法,就能快速解决。面对植树问题我们应当怎么解决呢?接下来带各位考生来探讨下这个问题。
对于植树问题,首先我们可以通过植树方式的不同将其分成两大类型,第一大类型是在一个非封闭的路线上植树,我们可以形象的将它理解为在一条笔直的马路上植树。第二大类是在一个封闭的路线上植树,我们可以将它理解为在一条环形的首尾相接的马路上植树。
首先对于第一种植树方式又可以大致分为三种,我们可以一起探究下:
1.道路不封闭且一端植树(道路首尾不相接,且道路的首尾处仅有一处种植一棵树,树与树之间有相同的间距)
公式:棵树=总路程÷间距
例:从纪念塔到电影院的路上共有1000米,每隔10米放一盆花,问总共可以放多少盆?(纪念塔下有一盆,电影院门口没有)
【解析】:由题干可知,种植方式为在不封闭的马路上每隔10米放置花盆,且路的一端纪念塔处可放置花盆。可知题目为:路不封闭且一端植树问题。根据公式可得:总共有=1000÷10=100盆。
2.路不封闭且两端都植树(道路首尾不相接,且道路的首尾处各种植一棵树,树与树之间有相同的间距)
公式:棵树=总路长÷间距+1
例:有一条堤全长500米,从头到尾每隔5米种植白杨树一棵,一共可以种( )棵。
A.100 B.101 C.99 D.102
【解析】:由题干所描述植树方式可知,题目为路不封闭且两端植树问题。已知每隔5米植树一棵,则一共可以种500÷5+1=101棵树。
3.道路不封闭且两端都不植树(道路首尾不相接,且道路的首尾处都不种植树,树与树之间有相同的间距)
公式:棵树=总路长÷间距-1
例:两座楼之间相隔56米,每隔4米栽一棵树,问一行能栽多少棵树?
【解析】由题干所描述植树方式可知,题目为路不封闭且两端都不植树问题,因为树只能在两个楼的中间植,所以,树的数目=56÷4-1=13棵。
其次对于封闭式植树的考察,我们可以这样理解:
封闭式植树指的是道路首尾相接,且树与树之间间距相等。
公式:棵树=总路程÷间距
例:在一周长为50米的花坛周围种树,如果每隔5米种一棵,共要种多少棵树?
A.10 B.11 C.12 D.15
【解析】:由题干所描述植树方式可知,题目为封闭区域植树问题。所以,花坛周围可种50÷5=10棵树。
以上是对于在考试中我们常见植树问题的简单归纳,较为复杂的植树问题也是基于这几种简单公式进行变型的。遇到植树问题我们可以先通过问题所描述的植树方式对其进行分类,找到其关键公式,再进行求解。
一元二次函数求最值
在备考公职类考试过程中,行测中的数量关系部分对于很多考生来说是最难的一部分,数量关系考查的题型有很多,比如行程问题、工程问题、极值问题、排列组合问题等等,难度也相对较大,但各位考生不必畏惧,把每一类问题逐一突破,让数量关系成为拿高分的杀手锏,今天重点来研究极值问题中的一类问题——一元二次函数求最值。

【例题】某期刊以每本2元的价格发行,可发行10万份。若该报刊单价每提高0.2元,发行量将减少5000份,则该报刊可能的最大销售收入为多少万元?
A.24 B.23.5 C.23 D.22.5
【解析】D。报刊销售收入=报刊单价×发行量,假设单价提高x次,报刊的销售总额收入为y,则y=(2+0.2x)(10-0.5x)。令y=0,得到x1=-10,x2=20,则当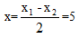 时,y有最大值y=(2+0.2×5)(10-0.5×5)=22.5,选择D选项。
时,y有最大值y=(2+0.2×5)(10-0.5×5)=22.5,选择D选项。
【例题】有一厂家生产销售某新型节能产品,产品生产成本是168元,销售定价为238元,一位买家向该厂家预定了120件产品,并提出如果产品售价每降低2元,就多订购8件。则该厂家在这笔交易中所获得的最大利润是( )元。
A.17920 B.13920 C.10000 D.8400
【解析】C。总利润=单利润×销售量,原利润=238-168=70元,假设一共降价x次,总利润为y元,则y=(70-2x)(120+8x),令y=0,得到x1=35,x2=-15,则当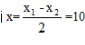 时,y有最大值y=(70-2×10)(120+8×10)=10000。选择C选项。
时,y有最大值y=(70-2×10)(120+8×10)=10000。选择C选项。
通过以上两道例题,相信各位考生应该对一元二次函数求最值问题有了大概的解题思路和方法了,一般来说,都是根据生活中的应用来设未知数列一元二次方程,而且是M=A×B型,所以顶点式可以更好地帮助考生求解一元二次函数最值问题。其实数量关系难度并没有想象中的那么大,把每一类特定题型掌握之后再通过练习,一定会让数量关系成为你成“公”之路的垫脚石。
运用基本结论,解决方阵问题
近年来,行测考试不断推陈出新,对比之前的常规题目而言,所测查考点在原有的基础上更加综合。今天给大家带来的是方阵问题的基本方法,其解题核心在于充分梳理题干条件,建立与基本结论之间的对应关系,进而求解的过程。方阵问题是我们数论问题的一种小题型,利用基本结论把文字描述转换成数学语言,进而解决实际问题。
一、 什么是方阵问题?
在方阵问题中,横的叫做行,竖的叫做列,如果行数和列数都相等,则正好排成一个正方形,就是所谓的“方阵”。
二、 方阵问题的基本特点
方阵分为实心方阵和空心方阵两种,方阵问题主要围绕方阵的层数、每层人数、总人数展开:
1、 每层每边人数依次增加2;
2、 每层人数依次增加8;
3、 每层的总人数=该层每边人数×4-4
4、 每层的每边人数=该层总人数÷4+1
三、 经典例题
例1:小明用围棋排成一个三层空心方阵,如果最外层每层有围棋子15个,小明摆方阵最里层共有多少个围棋子?
A.40 B.50 C.60 D.80
【答案】A。【解析】:由每层每边人数依次增加2,知最里层每边人数为15-2-2=11人,故该层总人数为11×4-4=40人,答案为A。
例2:有一队学生,排成一个中空方阵,最外层人数是52人,最内层人数是28人,这队学生共多少人?
A.140 B.150 C.160 D.180
【答案】C。【解析】:方阵外层每边人数=52÷4+1=14,内层每边人数=28÷4-1=6,中空方阵的总人数=14×14-6×6=160人,所以这队学生共160人,答案为C。
例3:学生分为甲、乙两个实心方阵,其中甲方阵最外层每边的人数为8。如果两队合并,可以另排成一个空心的丙方阵,丙方阵最外层每边的人数比乙方阵最外层每边的人数多4人,且甲方阵的人数正好填满丙方阵的空心。问学生一共多少人?
A.200 B.236 C.260 D.288
【答案】C。【解析】:由题意甲方阵总人数为82=64人,设丙方阵最外层为a,故总人数为a2-64=64+(a-4)2,解得a=18,故总人数为324-64=260人,答案为C。
随着公考的不断发展与变迁,数量关系的问题向着更综合的考查方向延伸,对于组成杂乱的数学问题我们要在平时的练习中多加积累,对于基本的结论要做到运用自如,个别情况下可以与方程的基本思想充分结合,会给解题带来更多的便捷。








