在国考行测数量关系中，计算问题每年都会被考查，最小公倍数就是计算问题中比较基础的考点，考查方式在考试中比较灵活。接下来为同学们分享如何巧用最小公倍数解计算问题。
一、什么是最小公倍数
如果一个自然数a能被自然数b整除，那么称a为b的倍数，例如6是3的倍数。两个或两个以上的自然数中，如果它们有相同的倍数，这些倍数就是它们的公倍数。例如12是3和4的公倍数。若干个数的公倍数中最小的一个就称为这若干个自然数的最小公倍数。
二、常见找最小公倍数的方法
找最小公倍数一般用分解质因数法和短除法。
1、分解质因数法：先分解质因数，再将所有的质因数取幂指数最大值连乘到一起，即为最小公倍数。
2、短除法：短除法求最小公倍数，先用这几个数的公约数去除每一个数，再用部分数的公约数去除，并把不能整除的数移下来，一直除到所有的商中每两个数都是互质的为止，然后把所有的除数和商连乘起来，所得的积就是这几个数的最小公倍数。
三、实战演练
例1：甲每5天去一次超市购物，乙每7天去一次，丙每11天去一次，某天3人在超市相遇，那么三人下次相遇至少需要多少天?
A.11 B.35 C.77 D.385
【参考解析】D。下次相遇经过的天数，分别应是5、7、11的倍数，相遇需要最少的天数即三者的最小公倍数。5、7、11的最小公倍数为5×7×11=385，故三人下次相遇至少需要385天。
例2：甲、乙、丙、丁四人去健身房的规律如下：甲每2天去一次，乙每3天去一次，丙每4天去一次，丁每5天去一次，上周星期日四人在健身房一起健身，下次四人一起去健身房是星期几?
A.星期四 B.星期五 C.星期六 D.星期日
【参考解析】A。2、3、4、5的最小公倍数为60。星期每7天一循环，60÷7=8 ……4，故下次四人同日去健身房健身是星期四。
多人相遇问题是考察最小公倍数最常见的题型，同学们在复习过程中掌握题型特征，熟悉解题方法，就可以快速解出题目答案。要想在考场上快速实现一分钟解决计算问题，还需要加强日常练习，保证熟能生巧。
多者合作怎么办，特值大法来帮忙
在本文中对常考考点多者合作问题进行方法介绍，多者合作研究的是多个主体通过一定方式合作完成工作的问题，利用工作总量等于每阶段工作效率与工作时间乘积的累加建立等量关系即可解决。在解决这类问题时，经常可以通过设定工作总量或者工作效率的特值来解决。给大家介绍两种最常见的特值方法，相信大家一定一学就会。
方法一：已知多个主体完工时间，一般将工作量设为1或多个完工时间的公倍数。
例题：
1.有两箱数量相同的文件需要整理，小张单独整理好一箱文件要用4.5小时，小钱要用9小时，小周要用3小时。小周和小张一起整理第一箱文件，小钱同时开始整理第二箱文件。一段时间后，小周又转去和小钱一起整理第二箱文件，最后两箱文件同时整理完毕，则小周和小张、小钱一起整理文件的时间分别是( )。
A.1小时，2小时 B.1.5小时，1.5小时
C.2小时，1小时 D.1.2小时，1.8小时
【参考解析】答案选A。设每箱文件的工作量是45，则总的工作量是45×2=90，小张、小钱、小周每小时分别整理10、5、15。由90÷(10+5+15)=3，即3小时后同时完成工作。第一箱文件，小张整理了10×3=30，则小周整理了45-30=15，整理了15÷15=1小时，故本题选A。
方法二：已知多个主体效率关系时，一般根据效率关系将效率最简比设为份数。
2.甲、乙两台洒水车合作给一片花园洒水，7小时可以完成。两洒水车共同合作5小时后，甲队所有队员及乙队人数的
调走去洒其他花园，又经过6小时，全部洒完，甲队单独给这片花园洒水需要( )小时。
A.12 B.15 C.10 D.20
【参考解析】答案选A。根据题意可得，甲、乙合作2小时的工作量和乙的人数工作6小时的工作量相等，即
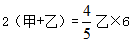，化简可得甲、乙效率比为7：5。设甲的效率为7，乙的效率为5，甲队单独给这片花园洒水需要
。故本题选A。
利润问题的常用解题方法
国家公务员行测考试中，利润问题是比较常见的题型之一，需要考生掌握利润问题的相关公式以及了解利润问题的常见解题方法，在考场上得分是相对比较容易的。利润问题与我们生活息息相关，主要是指在经济生活中，涉及成本、售价、利润、利润率以及折扣这几个基本的概念。今天带大家来了解利润问题的常用解题方法。
一、常用公式
1. 利润=售价-成本=成本×利润率
2. 售价=成本+利润=成本×(1+利润率)
3. 成本=售价-利润=售价/(1+利润率)
4. 利润率=利润/成本=售价/成本-1
5. 总价=单价×数量 、总利润=单利×数量
6. 折后售价=折前售价×折扣
二、常用解题方法
1. 方程法
方程法主要是根据题干中描述的等量关系，通过设未知量来建立方程，求解得到正确答案的一种方法。
例1
老王两年前投资的一套艺术品市价上涨了50%，为了尽快出手，老王将艺术品按市价的八折出售，扣除成交价5%的交易费用后，发现与买进时相比赚了7万元。问老王买进该艺术品花了多少万元?
A.42 B.50 C.84 D.100
【参考解析】B。设成本为x万元，根据条件描述，关系如下表所示：
成本 | 利润率 | 售价 | 利润 |
x | 50% | x×（1+50%）×0.8 | 7 |
由“发现与买进时相比赚了7万元”可建立等量关系为：x×(1+50%)×0.8×(1-5%)-x=7，解得x=50，即艺术品的成本价为50万元，选择B选项。
2. 特值法
特值法是指当题干中只有相对量而无绝对量，所求为乘除关系时，可设某个未知量为特殊的值从而简化计算的一种方法。
例2
某商店花10000元进了一批商品，按期望获得相当于进价25%的利润来定价，结果只销售了商品总量的30%，为了尽快完成资金周转，商店决定打折销售，这样卖完全部商品后，亏本1000元，问商店是按定价打几折销售的?
A.九五折 B.七五折 C.六折 D.四八折
【参考解析】C。由题干可知，10000元购进商品，且数量和成本未知，设一共购进了一件成本为100元的商品共100件。其具体关系如下表所示：
总成本 | 数量 | 单件成本 | 单价 | 总售价 | |
计划 | 10000 | 100 | 100 | 125 | |
前30件 | 3000 | 30 | 100 | 125 | 30×125=3750 |
后70件 | 7000 | 70 | 100 | 10000-1000-3750=5250 |
剩下的商品按原计划应该售出70×125=8750元，但实际全部商品卖出后售价为5250元。5250÷8750=0.6，即打了6折，选C选项。
流水行船问题快速解题技巧
行测考试中的行程问题，一直是令大家比较头疼的题型。但，并不是所有的行程问题都是特别复杂的。有一类特殊的行程问题，相对来说还是比较友好的，不会特别复杂，它就是流水行船问题。
一、什么是流水行船问题
在江河里航行时，除了本身的前进速度外，还受到流水的推送或顶逆，在这种情况下计算船只的航行速度、时间和所航行的路程，叫做流水行船问题。
二、流水行船问题的基本计算关系
顺水速度=船速+水速;逆水速度=船速-水速。(船速是指船在静水状态下的速度)
三、流水行船问题的解题技巧
由这两个基本的计算关系可以得到：顺水速度+逆水速度=2*船速，也就是说无论水速如何变化，顺水速度与逆水速度的和都是两倍的船速;顺水速度-逆水速度=2*水速，也就是顺水速度与逆水速度的差值是2倍的水速。这就是流水行船问题的解题核心所在。
四、流水行船问题的解题技巧应用
例1：一艘船往返于甲乙两港口之间，已知水速为8千米/时，该船从甲到乙需要6小时，从乙返回甲需9小时，问甲乙两港口的距离为多少千米?
A.216 B.256 C.288 D.196
参考解析：选C。在距离相同的情况下，速度比等于时间比的反比，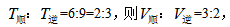
根据顺水速度-逆水速度=2*水速，假设顺流速度3份，则为水速0.5份对应8km/h，所以顺水速度3份对应为48，顺水时间为6小时，总距离=48×6=288千米，故选C。
例2：一艘船从A地行驶到B地需要5天，而该船从B地行驶到A地则需要7天，假设船速、水流速度不变，并具备漂流条件，那么船从A地漂流到B地需要几天?
A.40 B.35 C.12 D.2
参考解析：选B。在距离相同的情况下，速度比等于时间比的反比，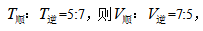
根据顺水速度-逆水速度=2*水速，假设顺流速度7份，则为水速1份。
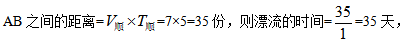故选B。
