
行测判断推理之联言命题推理知识点
一、联言命题的概念
复言命题是由逻辑联结词联结若干个命题而成的命题。构成复言命题的命题称为肢命题。根据逻辑联结词的不同,我们可以将复言命题分为联言命题、选言命题、假言命题和负命题四种。本节我们就先讲解下联言命题。
联言命题是陈述事物同时存在的命题,一般的形式为“p并且q”,联结词除了“并且”之外还有:“……和……,不但……而且……,虽然……但是……,不是……而是……”。
例如:国家和地方的公务员我都要考。这就是个联言命题,表示的是我同时要考国家和地方的公务员。“国家的公务员我要考”和“地方的我要考”是两个肢命题,称为联言肢。
注意:并存关系不是并列关系,并存只是表示同时存在,转折、递进等都是并存关系。
二、联言命题的真假关系
一个联言命题的真假与其肢命题的真假是密切相关的。因为联言命题的肢命题间是并存关系,所以只有肢命题同时存在,都为真的时候,联言命题才为真;只要其中一个肢命题为假,这个联言命题就为假。
简言之就是“全真才真,一假即假”。
例题:
北方人不都爱吃面食,但南方人都不爱吃面食。
如果已知上述第一个断定真,第二个断定假,则以下哪项据此不能确定真假?( )
Ⅰ.北方人都爱吃面食,有的南方人也爱吃面食
Ⅱ.有的北方人爱吃面食,有的南方人不爱吃面食
Ⅲ.北方人都不爱吃面食,南方人都爱吃面食
A.只有Ⅰ B.只有Ⅱ C.只有Ⅲ D.只有Ⅱ和Ⅲ
【答案】D【解析】题干中“北方人不都爱吃面食”等值于“有的北方人不爱吃面食”;“南方人都不爱吃面食”为假,意味着“有的南方人爱吃面食”为真。观察Ⅰ、Ⅱ、Ⅲ几个项,都是联言命题,要判定它们真假,就要充分利用其与其肢命题的真假关系“一假即假,全真才真”。
Ⅰ中肢命题“北方人都爱吃面食”为假,所以Ⅰ假。Ⅱ中肢命题“有的北方人爱吃面食”和“有的南方人不爱吃面食”均推不出它们的真假,因此也无法断定Ⅱ的真假。Ⅲ中肢命题“北方人都不爱吃面食”和“南方人都爱吃面食”也均推不出它们的真假,因此也无法断定整个联言命题的真假。所以,正确答案是D。
三、联言命题推理
如果一个联言命题为真,可以推出其任意一个肢命题都为真;同样,全部肢命题都为真,自然可以得到整个联言命题为真。
由联言命题为假,若一个肢命题外的其他命题都为真,可以肯定这个肢命题为假;如果其中一部分为假,则不能断定其他命题的真假。
“国家和地方的公务员我都要考”,这个联言命题可以进行如下推理:
国家和地方的公务员我都要考=>国家的公务员我要考;
国家和地方的公务员我都要考=>地方的公务员我要考;
国家的公务员我要考,地方的公务员我要考=>国家和地方的公务员我都要考。
四、选言命题的概念及分类
选言命题是陈述事物存在情况的命题,事物的存在情况可以分为两种,一种就是至少有一种情况存在,可能有很多不同的组合,这种命题叫做相容选言命题,一般形式为“p或者q”,联结词除了“或者”之外还有:“……或……,可能……也可能……,也许……也许……”;
还有一种是表示只能有一种情况存在,这种就称之为不相容选言命题,一般形式为“要么p,要么q”,联结词除了“要么……要么……”之外,还有“或……或……,二者不可兼得”。
注意:相容选言命题和不相容选言命题不能仅仅依靠联结词来区分,关键是要看其中各个肢命题能否同时成立:能够同时成立的就是相容选言命题,不能够同时成立的就是不相容选言命题。
例如:“她或者考国家公务员,或者考地方公务员”中“考国家公务员”和“考地方公务员”是可以同时成立的,即她可以既考国家的又考地方的,所以这个命题是相容选言命题。
而“你或者去面试,或者不去面试”中“去面试”和“不去面试”是不能同时成立的,即你不可能既去面试又不去面试,因此这个命题是不相容选言命题。
五、选言命题的真假关系
(一)相容选言命题真假关系
首先我们来看一下怎么来判断一个相容选言命题的真假。还是要从定义入手,相容选言命题要求至少有一个肢命题为真,因此:如果选言肢有一个为真,则相容选言命题就为真;只有当选言肢都为假,相容选言命题才为假。
简言之即“一真即真,全假才假”。
那么,“她或者考国家公务员,或者考地方公务员”这个相容选言命题,只要她参加了一场公务员考试那么就是真的;只有她既没参加国家公务员考试也没参加地方公务员考试的时候才为假。
例题1:某单位要从100名报名者中挑选出20名献血者进行体检。最不可能被挑选上的是1993年以来已经献过血,或是1995年以来在献血体检中不合格的人。
如果上述断定是真的,那么以下哪项所言及的报名者最有可能被选上( )?
A.小张1995年献过血,他的血型是O型,医用价值最高
B.小王是区献血标兵,近年来每年献血,这次他坚决要求献血
C.小刘1996年报名献血,因“澳抗”阳性体检不合格,这次出具“澳抗”转阴的证明,并坚决要求献血
D.大陈最近一次献血时间是在1992年,他因工伤截肢,血管中流动着义务献血者的血。他说:“我比任何人都有理由献血”
【答案】D【解析】题干中断定了一个相容选言命题,这个命题为真,则肢命题至少一个为真,即“1993年以来献过血的人”和“1995年以来在献血体检中不合格的人”,只要满足其中一个条件,就属于最不可能被挑选上的人。四个选项中,只有D项大陈两个条件都不能满足,不属于最不可能被挑选上的人,所以最有可能被挑选上。所以,正确答案是D。
例题2:三分之二的陪审员认为证人在被告作案时间、作案地点或作案动机上提供伪证。
以下哪项能作为结论从上述断定中推出( )?
A.三分之二的陪审员认为证人在被告作案时间上提供伪证
B.三分之二的陪审员认为证人在被告作案地点上提供伪证
C.在被告作案时间、作案地点或作案动机这三个问题中,至少有一个问题,三分之二的陪审员认为证人在这个问题上提供伪证
D.以上各项均不能从题干的断定推出
【答案】D【解析】由题干中的逻辑联结词“或”,可以知道题干是一句相容的选言命题。根据相容选言命题与其肢命题之间的真假关系,可以知道,只要一个选言肢为真,则可以推出整个相容选言命题为真;由相容选言命题为真,可以推出至少有一个选言肢为真,但是却不能推出是哪个选言肢为真。因此选项A和B都是不正确的。选项C具有很大的迷惑性,C项的错误在于三分之二陪审员有可能是分别认为三个选言肢正确的陪审员加起来的总和。因此排除C选项。所以,正确答案是D。
(二)不相容选言命题真假关系
由于不相容选言命题要求只能有一个选言肢为真,因此:如果选言肢有且只有一个是真的,则该不相容选言命题是真的;如果两个选言肢都是真的或者都是假的,则该不相容选言命题是假的。
简言之即“有且只有一真才为真;同真或同假时均为假”。
例题:某司机驾驶违章,民警说:“对你要么扣照,要么罚款。”司机说:“我不同意。”
那么,按照司机的说法,以下哪项他必须同意( )?
A.扣照,但不罚款
B.罚款,但不扣照
C.如果不能做到既不扣照又不罚款,那么就既扣照又罚款
D.承认错误,下次不再违章
【答案】C【解析】“要么扣照,要么罚款”是一个不相容选言命题,司机不同意这个说法,即该命题为假。而不相容选言命题在前件和后件同时为真或同时为假时均为假,即“既不扣照也不罚款或扣照且罚款”,再根据相容选言命题的推理规则,可知C项是正确的。因此,答案选C。
联言/选言命题
联言与选言
复言命题:几句话通过联结词的形式联结起来。
1.联言:就是通过“且”这个词连结。
P且Q(同义词连接)
口诀:“且”命题,全真才真,否则就假。(2个)
P且Q为真,P为真=>Q为真
P且Q为假,P为假=>Q为假
2.相容选言:“或”命题。本质是选择命题。
P或Q
口诀:“或”命题,有真就真,全假才假。(≥1个)
P或Q为真,P为假=>Q为真
P或Q为假,P为假=>Q为假
3.不相容选言:要么……要么……,不是……就是……
口诀:有么有且仅有一个要件为真。(一个)
且+要么=或——推一否一,一真一假
4.选言联言相互之间的转化。且与或本身就是一对转化词。和所有与有的、必然与可能是一个道理,均为翻硬币体系中的转化词。
矛盾公式:-(P或Q)=>-P且-Q;A且-B=>-A或B。
A或B≥1(有些)=>-A且-B=0(所有)
假言命题
假言命题:关联词进行连接的两句话。内在的逻辑关系是“=》”推出关系;例如:如果A,那么就B。
秒杀技巧:因为假言命题中,推出关系多种多样,为保证有效掌握,只记忆只有,才;除非,否则这两组词即可。
命题趋势:不出现关联词的情况
一般情况下,没有严格的关联词,都是前推后。但是要注意:充分、前提条件、基础、必要等字眼。
一、p是Q的充分条件。是p=>Q的形式。充分在前。
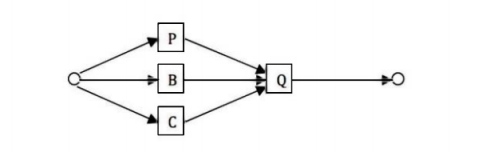
二、P是Q的必要条件;P是Q的基础:P是Q的前提条件。是Q=>P的形式。必要在后。

秒杀口诀:谁是充分谁在前;谁是必要谁在后。
三、A=》B的逆否命题
其实质是一种等价命题。我们讲过矛盾是翻动硬币一次。而等价是翻动两次。(仍然是翻硬币体系的运用)
所以,变为等价命题就必须动两次。
第一步:动符号。-A=>-B
第二步:动位置。-B=>-A
推出题:主要是表现为题干问法为推出,此时要区分题干较长,还是题干较短,较短直接做,较长逆向做。
三种命题的相互转化关系
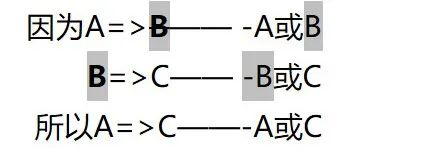
假言A=>B,它的矛盾命题是联言A且非B。而这个联言命题的矛盾命题是选言-A或B
矛盾的矛盾是等价:硬币翻了两次。所以,假言A=>B的等价是选言一A或B
转化口诀:A=>B矛盾命题是A且非B;A=>B等价命题是-A或B。

正负约分法
1.何时转化判断法则:选项为判断真假时,则推出转化为或/且;选项判断为推出关系时,则或/且转化为推出。
2.矛盾题与正负约分题区别:矛盾题题干有真有假;正负约分题题干全为真命题。
3.正负约分法步骤:
第一步:钥匙法:“钥匙”=真命题,用真去推其相关命题的真假,逐步得出结论(推出关系)。
第二步:题干“或”为主用正负约分法。
第三步:题干“非”“或”为主用正向代入法,前提是要件都为真,用不能转换的要件去排除选项。








