政华教育

提及行测朴素逻辑时，各位小伙伴都会觉得它“名不副实”，一点都不朴素，不知道该从何下手，做起来浪费时间，正确率也不高，所以在考试的过程中往往会选择放弃。朴素逻辑如果大家按照做其他的推理题目的方式从题干入手，会发现需要的时间比较长，所以这一次我们反其道而行之，从选项入手，学习一种方便快捷的解题方法——代入排除法。

什么是代入排除法呢？

代入排除法，一是代入法，可以把题干中的限制条件代入选项，不符合的选项直接排除，最终选出正确答案；二是排除法，可以根据选项给定的情况，将选项逐一代入题干中验证，如果代入后与题干中给定的条件相冲突，则排除，直至选出正确答案。

那我们什么时候用它呢？

当选项给出的对应关系较为全面或题干条件不确定时，可以考虑使用代入排除法。

我们简单拿两道题目试一下：

例1：在年终考评中，黄某带领的团队7人中有4人被评为优秀。已知：

（1）黄、丁、陈3人中有2人是优秀；

（2）李、杨、肖、贾4人中有2人是优秀；

（3）如果杨、贾两人中有人被评为优秀的，则陈也是优秀。

根据以上陈述，可以得出以下哪项？（）

A.陈、肖中至少有1人被评为优秀

B.黄、李中至少有1人被评为优秀

C.丁、肖中至少有1人被评为优秀

D.丁、李中至少有1人被评为优秀

【答案】A【解析】题干信息较为确定，可从选项代入解题。假设A项错误，陈、肖两个人都没有被评为优秀，根据条件（3）可知杨、贾没有被评为优秀，此时肖、杨、贾都没有被评为优秀，无法满足条件（2）的要求，则假设不成立，A项正确。故本题选A。

例2：甲、乙、丙、丁4位同学参加学校运动会。已知他们4人每人都至少获得1个奖项，4人获奖总数为10。关于具体获奖情况，4人还有如下说法：

甲：乙和丙的获奖总数为5；

乙：丙和丁的获奖总数为5；

丙：丁和甲的获奖总数为5；

丁：甲和乙的获奖总数为4。

后来得知，获得2个奖项的人说了假话，而其他人均说了真话。

根据以上信息，甲、乙、丙、丁4人具体的获奖数分别应是：（）

A.2、3、2、3 B.2、4、1、3

C.2、2、2、4 D.2、2、3、3

【答案】C【解析】题干信息和选项均较为确定，可从选项入手解题。观察4个选项发现，甲的获奖数都是2，再结合题干信息可知，获得2个奖项的人说了假话。由此可知甲说了假话，那么乙和丙的获奖总数不是5。再回归选项可发现，只有C选项的乙和丙的获奖总数不是5，故本题选C。

直击朴素逻辑的本质

在行测考试中朴素逻辑几乎是必考题，一说到朴素逻辑题大家可能就有点望而却步，心生畏难情绪。一杯酒一支烟，一个逻辑推一天，要不然，还是放弃吧？这是大家的一个初印象，但朴素逻辑题也是有套路的，简单来说就是元素的对应。最终考查的本质就是元素要一一对应，归根结底，有迹可循。下面就跟大家来聊一聊。

朴素逻辑的题目中，题干会给定很多信息，我们需要从众多信息中找到解题的切入点，即找到做题突破口进而快速解题。突破口：找突破口是解朴素逻辑的核心解题思路，以“确定性、关联性”作为突破口入手。那么什么是确定性和关联性呢？

1.确定性

即是通过题干中一句话即可得到结论或得到相对确定的结论的信息。比如“菊说我是三姐，竹说兰不是三姐”，前半句就是确定性信息，应该优先从前半句切入解题，再结合关联性进一步巧解题目。

2.关联性

关联性信息分为高频信息与多维度信息，其中高频信息是指多次出现的信息；多维度信息是指一句话包含多种元素信息。比如：甲比医生大，其实在告诉我们甲不是医生。通过这两个解题方法去找到元素之间的对应关系。下面我们来通过一道题目讲一下如何更好地应用突破口来快速解决复杂的朴素逻辑题目。

例题：某宿舍有A、B、C三人，一个出生在湖南，一个出生在湖北，一个出生在天津，他们所学的专业，一个是金融，一个是管理，一个是外语。已知：

①B不是学外语的

②B不出生在天津

③C不出生在湖南

④学习金融的不出生在湖北

⑤学习外语的出生在湖南

根据上述条件，可推出A所学的专业是：（）

A.金融 B.管理 C.外语 D.推不出

【答案】C【解析】条件⑤的确定性最强，以⑤为突破口解题。⑤包含外语和湖南两类元素，条件①也包含外语，结合⑤①可知，B不出生在湖南，条件③也包含湖南，结合⑤③可知，C不出生在湖南，可知A出生在湖南，学习外语，可知C项正确。也可继续推理，A的出生地确定后，结合②可知B出生在湖北，C出生在天津。结合条件④可知，出生在湖北的B不学习金融，则B学习管理，C学习金融。故本题答案选C。

这道题我们就是利用了突破口的两个信息，先找到确定性再结合关联性解决题目，此题中题干中条件⑤给出的内容最为确定，所以可以从条件⑤入手结合其他条件做进一步推断，最终推导出正确答案。

所以对于朴素逻辑，我们一定要善于利用确定信息，以此为突破口，然后结合其他关联性的信息解题，希望考生们多多进行题目训练，从而拿下这一类题型。希望通过这道题目能够让各位小伙伴对于可能性推理中朴素逻辑题目有更好的体会，快去找些题目练习一下吧。

行测朴素逻辑如何突破

在行测判断推理中，朴素逻辑属于重点必考题型，朴素逻辑不同于命题推理，没有明确的规则可以套用，但是我们也可以从题目所给的条件中总结出来一些解题的突破口。今天就为大家带来朴素逻辑的解题思路点拨，希望能够帮助大家更高效地掌握朴素逻辑的作答思路。

突破口一：确定性信息

当题干所给条件较多时，应尽快找到确定内容进行推理。

例1：有四个人，他们分别是小偷、强盗、法官、警察。第一个人说：“第二个人不是小偷。”第二个人说：“第三个是警察。”第三个人说：“第四个人不是法官。”第四个人说：“我不是警察，而且除我之外只有警察会说实话。”

如果第四个人说的是实话，那么以下说法正确的是：（）

A.第一个人是警察，第二个人是小偷

B.第一个人是小偷，第四个人是法官

C.第三个人是警察，第四个人是法官

D.第二个人是强盗，第三个人是小偷

【答案】D【解析】根据最后一句可以确定丁说的是真话，甲乙丙中有人是警察。假设第三个人确实是警察，则第二个人说的是真话，第二个人也是警察，与题意矛盾。由此可知第三个人不是警察，第三个人说的是假话，第四个人是法官。因为已知第三个人不是警察，所以第二个人说的也是假话，第二个人也不是警察，则警察是第一个人。因为只有警察说真话，可知第一个人说真话，第二个人不是小偷，是强盗，则第三个人是小偷。故答案选D。

突破口二：关联性信息

当题干没有确定信息时，可以从关联性入手，找高频信息。

例2：幼儿园马老师和三个小朋友情情、可可和安安一起玩“猜一猜，我最棒”游戏，马老师对小朋友们说：“我把手中的红球、黄球和蓝球分别放在这个柜子的三个抽屉里，请你们猜一猜每只抽屉里放的是什么颜色的球？猜对了奖励小红花！”然后，她请小朋友们闭上眼睛，把三只球分别放在三个抽屉里，小朋友猜的情况如下：

情情说：“红球在最上层的抽屉，黄球在中间抽屉。”

可可说：“红球在中间抽屉，蓝球在最上层的抽屉。”

安安说：“红球在最底层的抽屉，黄球在最上层的抽屉。”

老师告诉她们，每人都只猜对了一半。

请问：红球、黄球和蓝球各在哪一层抽屉里：（）

A.红球在中间抽屉，黄球在最上层的抽屉，蓝球在最底层的抽屉

B.红球在中间抽屉，黄球在最底层的抽屉，蓝球在最上层的抽屉

C.红球在最上层的抽屉，黄球在最底层的抽屉，蓝球在中间抽屉

D.红球在最底层的抽屉，黄球在中间抽屉，蓝球在最上层的抽屉

【答案】D【解析】题干并无确定信息，可从最高频率出现的红球入手，关于红球有3种不同猜测，但只有1句是正确的，还有2句均错误。根据每人只猜对了一半可知，3个人后半句中，有2句正确、1句错误。而黄球有2种不同猜测，必有一句错误，所以关于蓝球的猜测必然正确，蓝球在最上层。则红球在最底层，黄球在中间。故本题应该选择D项。

巧用方法破解行测朴素逻辑一拖N题型

如果问行测哪种题目最难，应该能想到一种特殊的题型，就是朴素逻辑中的一拖N，一般以一拖五的形式考察，题目难度系数大。接下来和大家具体来看一下遇到这种题目该如何做。

例题：有甲乙丙丁戊五位员工，他们来自办公室、教育局、商务局、税务局和环保局五个部门，他们在周一到周五都要休息一天，而且每天只能安排一人休息。与此同时他们在篮球、足球、羽毛球、乒乓球和保龄球这五种运动里都有自己唯一的爱好，且爱好各不相同。已知条件如下：

①周二休息的人喜欢打篮球，但他不是来自办公室的甲

②乙非商务局工作人员，且不喜欢打羽毛球和篮球；

③丙周三休息，丁和戊均不在周四休息；

④丁在环保局工作，戊在税务局工作；

⑤周一休息的人喜欢打乒乓球；

看到题干给的信息发现，各种关系太复杂了，接下来我们必须要做的事情就整理题中的各种关系，整理完如下表：

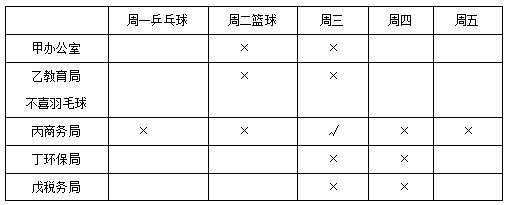
整理完成后，带着表格，我们对照每道题目，看如何解题。

1.以下哪一项陈述可能为真（）？

A.在环保局工作的人周四休息，喜欢踢足球

B.在商务局工作的人周三休息，喜欢打篮球

C.在教育局工作的人周二休息，喜欢打羽毛球

D.在税务局工作的人周一休息，喜欢打乒乓球

【答案】D【解析】根据上表可知，A项环保局工作的人不可能周四休息。B项商务局工作的人不可能喜欢打篮球。C项在教育局工作的人不可能在周二休息。D项在税务局工作的人是戊，可能周一休息，喜欢打乒乓球。

2.根据以上信息，丙可能喜欢的运动有（）？

A.足球、乒乓球、羽毛球、保龄球

B.篮球、保龄球、羽毛球

C.羽毛球、足球、保龄球

D.羽毛球、保龄球、乒乓球

【答案】C【解析】根据上表可知，丙在商务局工作，周三休息，不可能喜欢乒乓球和篮球，只有C项符合。

3.如果周四休息的人喜欢打羽毛球，那么以下哪项陈述一定为假（）？

A.甲在周四休息 B.甲喜欢乒乓球

C.丙喜欢打保龄球 D.丁喜欢打篮球

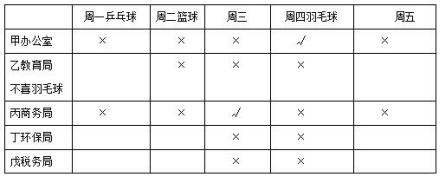
【答案】B【解析】由上表可知，甲在周四休息，喜欢羽毛球，一定不喜欢乒乓球，B项一定为假。

4.如果税务局工作的人员喜欢打保龄球，那么以下哪项陈述可能为真（）？

A.周五休息的人在教育局工作 B.周三休息的人员不喜欢踢足球

C.在环保局工作的人喜欢打乒乓球 D.在商务局的工作人员喜欢打篮球

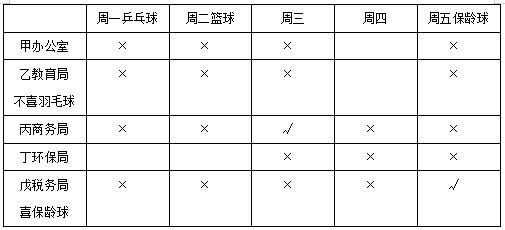
【答案】B【解析】由上表可知，A项周五休息的人是戊，在税务局工作。B项周三休息的人是丙，可能喜欢羽毛球，不喜欢踢足球，正确。C项在环保局工作的是丁，只能喜欢乒乓球或篮球。D在商务局工作的人是丙，周三休息，不可能喜欢打篮球。

5.如果甲和乙休息日隔了两天，那么以下哪项一定为假（）？

A.教育局的员工喜欢保龄球 B.税务局的员工喜欢乒乓球

C.丙喜欢保龄球 D.戊周二休息

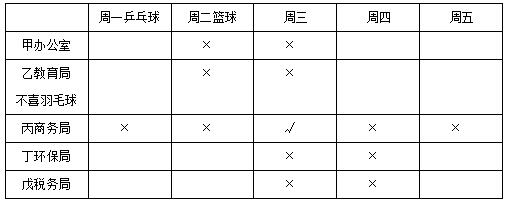
【答案】B【解析】由上表可知，甲乙相隔两天只能在周一和周四休息，则在戊税务局工作，不可能在周一休息，也就不可能喜欢乒乓球了，B项一定为假。

通过上面几道题目的分析我们发现，朴素逻辑的题目如果运用的方法得当，是可以做到快速准确做完的。其中的关键就是对题中信息的整理，利用题中的信息将题中的各种关系通过图表法罗列到纸上，再以其为模板，分题目推理，就可以快速的选出正确选项了。