行测图形推理：把握重点 快速得分

笔画问题

一笔画图形在近年公务员考试行测试卷中“出镜率”非常高，并且难度加大，因此，掌握好“一笔画”问题的解题方法和技巧，对于提高做题速度和准确率有很大帮助。然而很多考生在备考时看到一笔画图形感觉很茫然，究竟什么是一笔画图形呢？如何判定一笔画图形呢？下面带着大家一起来了解一下。

何为一笔画

所谓一笔画要满足三个条件：①笔不离纸②线不重复③走遍所有路径。

例如一个圆，一个正方形，都是明显可以一笔画出的图形，但是再复杂一些的图案，能不能一笔画就不好判定了。

很多同学拿到这样的题目习惯自己先去画一下，是不是能一笔画出，但是这样的方法只适用于极其简单的图形，如果图形的困难指数稍微大一些，比如下图，这样的图形仅凭观察无法直接看出是一笔画图形，那这样的方法便不适用了，是否有万能又简单易行的方法呢，接下来就给大家介绍方法。

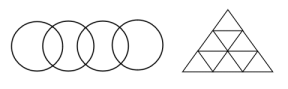
巧判一笔画

对于图形的笔画数有其判定公式，即笔画数=奇点数/2。其中具有0个或2个奇点的图形为一笔画图形。我们发现可以通过数奇点来判断图形是否为一笔画图形。

那么何为奇点呢？在图形当中从某一点出发的线条数，如果有奇数条，我们就称这样的点为奇点。注意端点也是奇点。我们一起来数一下

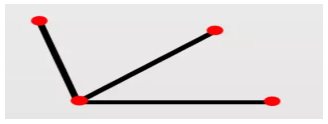
这幅图中的左上、右上以及右下的三个点，均分别只引出一条线，1是奇数，故这三个点均为奇点；左下角这个点，引出了三条线，3是奇数，所以左下角这个点也为奇点，所以上图一共4个奇点，就不能一笔画。明白了简单的判定方法，较为复杂的图案能否一笔画，我们也可以简单进行判定，例如下图：

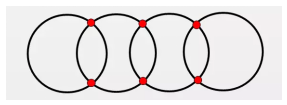
图案中虽然点较多，但是这6个点都分别引出了四条线，因为4是偶数，所以上图没有奇点，奇点数为0，故可以一笔画。

例题：把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：（   ）

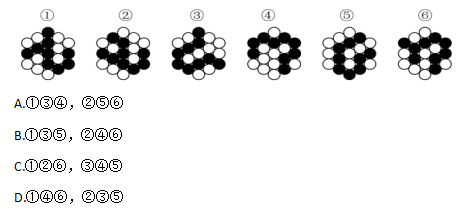
【答案】C【解析】第一步，观察特征。图形都由黑色小球和白色小球组成，且所有圆圈都连在一起，故有可能考虑自身特性或数量关系方向的规律。又黑色小球部分数均为1，考虑连线的笔画数的规律。第二步，根据规律进行分组。如下图所示，图形①②⑥中黑色小球的连线为2笔画，图形③④⑤中黑色小球的连线为1笔画，分为两组。

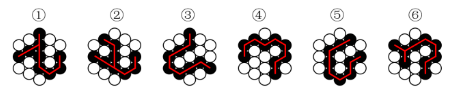
因此，选择C选项。

一笔画问题也是行测考试中的高频考点，当图形相异需要考虑数量关系的时候一定不要忽略一笔画问题这一考点。

“规律叠加”巧发现

在行测考试中，图形推理是一种必考题型，要求应试者从已给出的图形的排列方式中找出图形排列的规律，并根据这个规律推导出问号处应填上什么样的图形而不违背这个规律。从考点上看，转动、移动、叠加、几何特性、数量关系、图形的相对位置和立体图形等均有考查。这类试题主要考察抽象判断能力，因其很少受知识或文化背景的影响，故这类试题存在一定的难度。今天跟大家分享图形推理中的常考考点“叠加”规律，希望大家能够熟练掌握，从而提高做题效率。

“叠加”规律可具体分成四种常见小考点：

①直接叠加：第一个图形直接与第二个图形叠加，得到第三个图形。

②去同存异：第一个图形与第二个图形叠加，去掉相同的部分，留下不同的部分，得到第三个图形。

③去异存同：第一个图形与第二个图形叠加，去掉不同的部分，留下相同的部分，得到第三个图形。

④规律叠加：一般会在黑白格的基础上进行考察，比如图形对应相同位置的颜色变化规律：黑色+黑色=黑色、白色+白色=黑色、黑色+白色=白色+黑色=白色，找规律时，注意对应好同一个位置。但是有些题目也会在小图形的基础上考察规律叠加，大家要灵活应对。

接下来我们看几道例题来验证一下。

例题1：从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律：（   ）

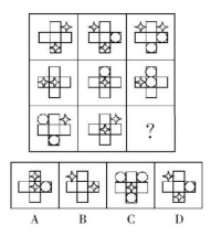
【答案】C【解析】观察前两行图形可以发现，前两个图形叠加得到第三个图形，叠加规律为：星星+空白=星星，星星+星星=圆，圆+空白=圆。

例题2：从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律：（   ）

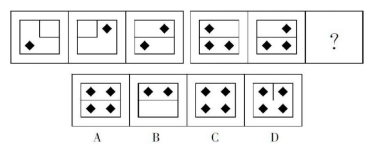
【答案】C【解析】每组前两个图形叠加，内部直线去同存异，黑色方块保留，故答案选择C。

由上面两道例题我们可以看出“叠加”类的考题难度不大但是需要细心。在解答图形推理题目时，首先要做到仔细观察题干图形，其次在考点的基础上找出规律，最后根据规律选择正确选项。

“俄罗斯方块”巧解立体拼接

行测图形推理中，立体图形中的立体拼接可能是比较头疼的题目了，甚至很多考生在备考时准备放弃此类题目了。其实立体拼接并不是洪水猛兽，只要掌握了做题方法，也不过是“纸老虎”，外强中干罢了，通过几个题目把一些常见的解题方法总结一下，助力大家一举打败这只“纸老虎”。

常见的方法有两种：一种是数量法，相对容易；一种是利用互补原则的试拼，也是我们这次主要学习的“俄罗斯方块”的解题方法。

先来看数量法，数量法简单讲就是数个数，即我们先看需要拼的立方体是由多少个小立方体组成，已知条件已经满足多少个，确定还缺少多少个，数量不符合的选项直接排除。我们以下面题目为例：

例1：下图为同样大小的正方体堆叠而成的多面体正视图和后视图，该多面体可拆分为①、②、③和④共四个多面体的组合，问：下列哪一项能填入问号处？（   ）

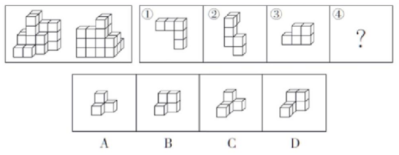
【答案】D【解析】第一步：先数一下最终要拼成的几何体一共由22个立方体组成；

第二步：已知1和2和3一共有个16小立方体，所以还需要6个立方体方能拼成，满足此个数要求的只有D项，因此该题选D。

数量法简单易懂，相信大部分考生能够轻松掌握。下面我们来看一下第二种，也就是“俄罗斯方块”的解法。“俄罗斯方块”我们通俗一点解释就是利用玩俄罗斯方块的思维，先选取合适的位置把已知的立体图形先拼接完成，再利用互补思想补齐即可，以下面的题目为例：

例2：从所给的四个选项中，选择最合适的一个填入问号处，使下图中的立体图形①、②、③和④可组成一个完整的长方体。（   ）

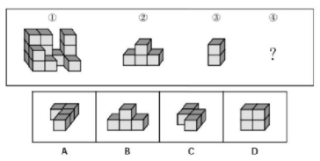
【答案】C【解析】通过题干可知，最终需要拼成的几何体为长方体，四个选项的个数都为4个，所以数量法不适用此题。具体的拼接过程我们分为如下几步：

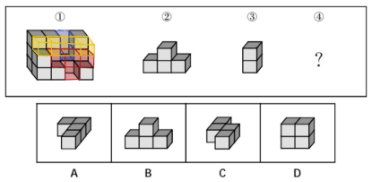
第一步，因为题干中第一个图形的个数比较多，我们以它为基准先把第二个和第三个拼接上去，比如下图这种情况，就会发现拼完之后还需要四个长条状的几何体（即黄色部分），但是没有此选项，说明位置放置错误。

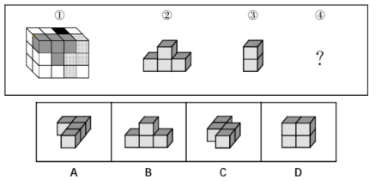
第二步：尝试一下第二个位置，也就是把题干中的第二个图形往上面移动一层，第三个不变（如下图所示），就会发现还需要一个竖着的“Z”型多面体方能补全，正好对应选项C，所以该题选C。

以上就是两种处理立体拼接题目的做法，希望对大家有所帮助。当然不仅仅是立体图形，所有图形推理的题目都需要大家通过大量题目的练习，达到“唯手熟尔”。所以行动起来，拿上武器，去推倒那些“纸老虎”吧！

立体拼接之多合一

图形推理这类题型在行测考试中每年都会考察，需要我们将其作为重点进行学习。其中立体拼接类的题目考试难度是相对较高的。按照需要拼接的图形部分数可将题型分为两类：二合一、多合一。对于这类题目，很考验我们的空间思维，在此围绕立体拼接中“多合一”这类题型给大家讲解一些小技巧。

一、选项方块数不一致，先数方块数

需要拼成的完整立体图形共由几个小方块组成是可以数出来的，而组成完整图形的每一部分的小方块数总和应该和完整图形总数一致。所以当我们观察到选项给出的部分小方块数不一样时，可以尝试直接数方块数排除答案。

下面我们来看一道题目：

【例】下图为同样大小的正方体堆叠而成的多面体正视图和后视图。该多面体可拆分为①、②、③和④共4个多面体的组合，问：下列哪一项能填入问号处？（   ）

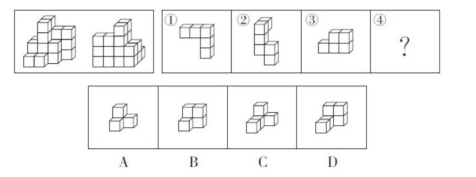
【答案】D【解析】观察立体图形的正视图和后视图可知，该立体图形由22个小正方体组成，而图形①②③中共有16个小正方体，还缺少6个小正方体，选项中A有4个小正方体，B有5个小正方体，C有5个小正方体，D有6个小正方体，只有D项符合。故本题选D。

二、选项方块数一致，分层绘图——试拼

当选项方块数一致时，无法用数数的方式进行排除，这个时候需要我们根据题干给出的完整图案进行试拼。但是直接进行拼接太考验空间思维，那么，有没有什么方法可以简单一点、直观一点辅助我们进行试拼呢？接下来给大家介绍一种小技巧——分层绘图。

任何一个由小正方体组成的立体图形我们都可以从上到下，从左到右，从前到后的分为几层。如果我们选取一个方向把图形剖开，分成几层，然后尝试把题干中已经给出的每一部分填入剖开的每一层里，那么最后填完题干已给所有的小正方体后剩下的空白部分所组成的图形就是我们要找的答案。

实际上，这种方法体现的是一种降维的思维，把立体的问题转化为平面的问题，化难为易。一方面可以帮助我们解决立体图形拼接的问题，另一方面通过降维思维的练习也可以锻炼我们的空间思维。

话不多说，我们拿一道题目来学习一下。

【例】左图给定的是由相同正方体堆叠而成的多面体。该多面体可以由①、②和③三个多面体组合而成，以下哪项能填入问号处？（   ）

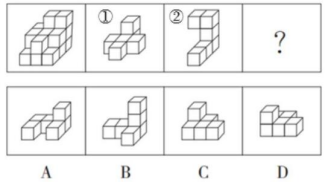
【答案】D【解析】观察题干图形，共分为3层。从下往上依次来看：第一层有9个小正方体，第二层有7个小正方体，第三层有2个小正方体。分层绘图如下：

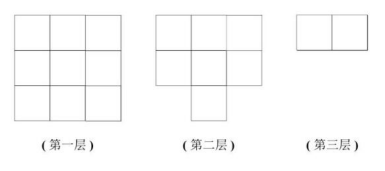
由于②的形状较为特殊，优先考虑放置，可放在多面体右侧，分层来看：

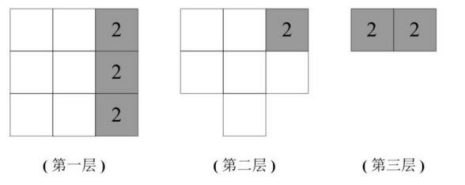
此时结合①的特征，由于按照图示放置时，①中右侧的位置已经②中的小方块占位，所以不能直接放置①，需要将①翻转如下图与②拼合。

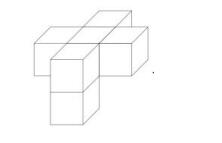
此时题干多面体的各层能确定的图形放置方式为：

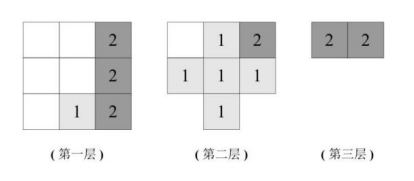
剩下空白区域为两层，且小立方体数量为5+1的多面体，观察选项，D符合。故本题选D。

通过今天的学习，我们了解了关于立体拼接类题目多合一这种题型的一些解题技巧，但是掌握技巧也需要我们多思考、多练习。每天一小步，成长一大步，在此祝愿诸君乘风破浪，直挂云帆济沧海！

黑白点”

在行测考试中图形推理是非常重要的一部分，从近年来行测考试的命题趋势看，黑白点、黑白格子以及阴影图形出现频率比较高，而像这种特征的题目常见的考法为位置变化或者规律叠加，但是有些题目我们试过后并不能找到规律，很容易影响做题心态，那么我们就需要打破思维定势，那就是用图形特征去寻找其他的规律，接下来带大家一起看看都有哪些规律吧！

笔画数

例1：把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：（   ）

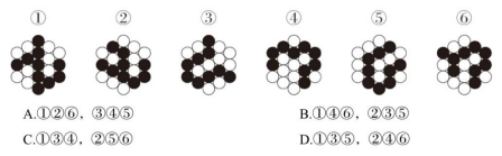
【答案】A【解析】题干图形均由黑点和白点组成，考虑两种圆圈的数量性和位置性规律均无法得到答案。进一步观察发现，黑色圆圈连成的图形均为一部分，有的可一笔画出，有的可两笔画出，可考虑笔画数规律。图形①②⑥中黑色圆圈连成的图形需两笔画出，图形③④⑤中黑色圆圈连成的图形可一笔画出。故本题选A。

部分数

例2：从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。（   ）

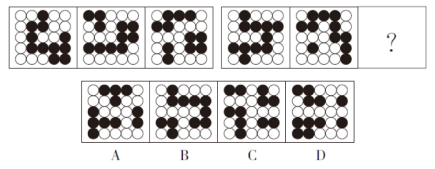
【答案】A【解析】题干图形均由黑色圆圈和白色圆圈组成，考虑两种圆圈的数量性和位置性规律，但是没有位置规律，考虑小黑球或者小白球的部分数，相连小黑球作为一部分，每组图形中，黑色圆圈部分数依次为1、2、3，选项中只有A项黑色圆圈部分数为3。故本题选A。

白块区域数

例3：把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项（   ）

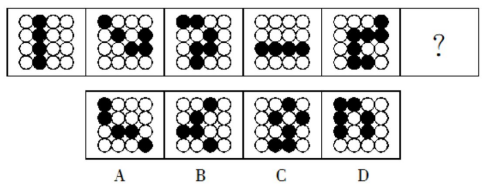
【答案】A【解析】黑点的位置关系和数量上均无法得到答案，进一步观察发现，黑色圆圈的连线将白色圆圈分为两个部分。选项中只有A符合这一特征。故本题选A。

对称性

例4：把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是（   ）

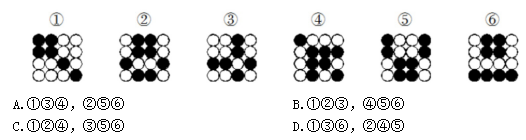
【答案】A【解析】整体观察题干图形，黑点的位置关系和数量上均无法得到答案，进一步观察发现黑格组成的图形均为轴对称图形，我们发现图形①③④中黑格组成的图形对称轴均为斜线，图形②⑤⑥中黑格组成的图形对称轴均为竖直线。故本题选A。

通过以上题目，大家可以发现“黑白点”除了常规考法外，还会考到笔画数、部分数、白块区域数、对称性等等，所以大家在平常的学习和做题中不要拘泥于常规规律，可以尝试多发散思维，根据图形不同的特点，找寻图推的新思路，同时大家一定及时做好总结，积累多种多样的规律之后，才能在考场上应对自如！