行测技巧：掌握技巧 高效突破朴素逻辑题

行测朴素逻辑列表连线巧辨析

行测朴素逻辑题目考查逻辑推理能力，多种元素的对应问题可以结合题干和选项情况采取不同方法，比如排除法、图表法和假设法。通常情况下，选项信息全面，一一对应，优先采用代入排除法。题干信息全面，涉及一类元素的顺序问题，直接结合顺序排列；题干有两类元素不涉及顺序，可采用列图表和连线法解决，优先采用列表法；题干涉及三类元素时优先用连线法解决。题干真假话情况不确定，采用假设法解决问题。重点讲解列表法和连线法，接下来结合题目来分析一下：

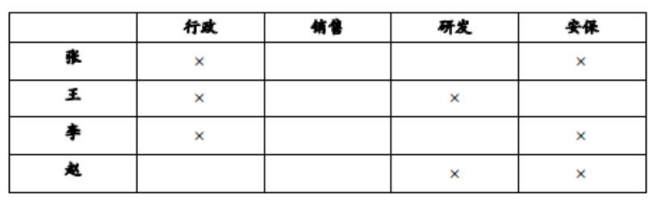
【例1】大学毕业的张、王、李、赵4人应聘到了同一家大型公司，每人负责一项工作。其中一人做行政管理，一人做销售，一人做研发，另一人做安保。已知：

①张不做行政管理，也不做安保；

②王不做行政管理，也不做研发；

③如果张没有做研发，那么赵也没有做行政管理；

④李不做行政管理，也不做安保；

⑤赵不做研发，也不做安保。

由此可以推出：（   ）

A.张做销售，李做研发

B.赵做研发，李做销售

C.李做销售，张做研发

D.李做研发，赵做安保

【解析】由条件①张不做行政管理，也不做安保，在表中打×；②王不做行政管理，也不做研发，在表格中打×；④李不做行政管理，也不做安保，在表中打×；⑤赵不做研发，也不做安保，在表中打×，列表如下，再结合张、王、李不做行政，赵做行政管理，同理王做安保，再由条件③假言命题知：赵行政管理推出张做研发，确定每个人情况。

上面的例题题干给出两类元素且不涉及顺序，采用列表法或者连线法，每个人的情况都能够在表格中确定。但如果题干给出三类元素，则二维表格不能解决问题，采用连线法。在采用连线法解决问题时要注意，有关用实线，无关用虚线。结合下面例题一起学习一下：

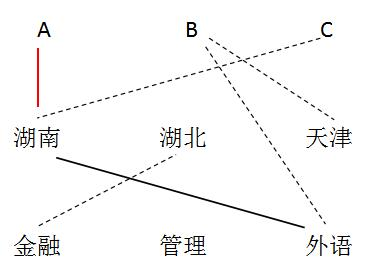
【例2】某宿舍有A、B、C三人，一个出生在湖南，一个出生在湖北，一个出生在天津，他们所学的专业，一个是金融，一个是管理，一个是外语。已知：

①B不是学外语的

②B不出生在天津

③C不出生在湖南

④学习金融的不出生在湖北

⑤学习外语的出生在湖南

根据上述条件，可推出A所学的专业是：（   ）

A.金融       B.管理      C.外语        D.推不出

【答案】C【解析】可使用连线法：结合题干信息，运用连线法，将存在对应关系的元素之间进行连线。由⑤学习外语的出生在湖南，结合①B不学习外语，③C不出生在湖南，可以确定A出生在湖南且学习外语。

这两个题主要是利用列表法和连线法，两个元素或者三个元素存在对应关系，采取适合的方法，对题干适当推理，结合朴素逻辑突破口就可以快速解决问题。

如何应对行测朴素逻辑中的“半真半假”问题

在行测判断推理朴素逻辑考查中，有一种“半真半假”的题型。考生们往往找不到解题的抓手，不仅费时而且还会影响考试情绪。那在这类“半真半假”的题型中，如何快速、高效破题呢？今天为大家推荐两种有效的解题思维。

“半真半假”题目会给我们3-5句不同人物的发言，每个人都会说涉及对应元素和条件的匹配的两句话，最后告诉我们，每个人的话都“只说对了一半”。这就是“半真半假”问题。那么面对这样的问题，我们便可以通过“反复使用题目中高频出现的信息”或者找到“涉及其他整个句子的半句必假”来快速解题，那这两种方法究竟如何应用呢？接下来通过两道经典的例题来感受一下如何在考场上快速解决“半真半假”问题：

方法一：抓高频信息并反复使用

【例1】幼儿园马老师和三个小朋友情情、可可和安安一起玩“猜一猜，我最棒”的游戏。马老师对小朋友们说：“我把手中的红球、黄球和蓝球分别放在这个柜子的三个抽屉里，请你们猜一猜每只抽屉里放的是什么颜色的球？猜对了奖励小红花！”然后，她请小朋友们闭上眼睛，把三只球分别放在三个抽屉里。小朋友猜的情况如下：

情情说：“红球在最上层的抽屉，黄球在中间抽屉。”

可可说：“红球在中间抽屉，蓝球在最上层的抽屉。”

安安说：“红球在最底层的抽屉，黄球在最上层的抽屉。”

老师告诉她们，每个人都只猜对了一半。

请问红球、黄球和蓝球各在哪一层抽屉里？（   ）

A.红球在中间抽屉，黄球在最上层的抽屉，蓝球在最底层的抽屉

B.红球在中间抽屉，黄球在最底层的抽屉，蓝球在最上层的抽屉

C.红球在最上层的抽屉，黄球在最底层的抽屉，蓝球在中间抽屉

D.红球在最底层的抽屉，黄球在中间抽屉，蓝球在最上层的抽屉

【答案】D【解析】通读题干信息，我们会发现题目告诉我们三位女孩的话都是“半真半假”，问我们最终三种颜色的球在抽屉的什么位置。观察题干中三位女孩的话，红球出现次数最多(三次)，但红球实际只能有一个位置，故三位女孩的前半句话中必然为1真2假；除红球外，黄球出现次数最多(两次)，故观察情情、安安两人的后半句话可知，黄球也只能有一个位置，关于黄球的两个半句中至少会有一句假话。再结合题干“半真半假”的信息，我们知道三个完整的句子中应有3个半句为真、3个半句为假。此时，就可以推知剩下的关于蓝球的这半句必然为真。因此，蓝球必然在上层。根据每个人的话都“半真半假”可知，“红球在中间”为假，那么红球必然在下层，故黄球在剩下的中间。故本题选D。

方法二：涉及到其他整个句子的半句必假

【例2】三人在一起猜测晚会节目的顺序。甲说：“一班第一个出场，二班第三个出场。”

乙说：“三班第一个出场，四班第四个出场。〞丙说：“四班第二个出场，一班第三个出场。”

结果公布后，发现他们的预测都只对了一半。

由以上可以推出，节目的正确出场顺序是：（   ）

A.四班第一，三班第二，一班第三，二班第四

B.二班第一，一班第二，三班第三，四班第四

C.三班第一，四班第二，二班第三，—班第四

D.一班第一，二班第二，四班第三，三班第四

【答案】C【解析】通读题干信息，我们会发现此题与例题1有相似之处，也是告诉我们四人的话都是“半真半假”。但是这道题缺少明显的高频信息，所以我们可以观察“涉及到其他整个句子的半句”，例如丙所说的后半句“一班第三个出场”，这个半句涉及到甲的整个句子(前半句“一班”和后半句“第三”)，假如丙的后半句为真，则一班就不可能第一个出场、第三个出场的也不可能是二班，此时甲的话全为假，与题干中“半真半假”不符合，故丙的后半句必然为假，则前半句必然为真，即四班第二个出场。观察选项，只有C项满足。故本题选C。

上述分享是想告诉各位为公考奋斗的同学们，对于朴素逻辑中“半真半假”的题目，我们可以“反复使用题目中高频出现的信息”，也可以通过找到“涉及到其他整个句子的半句必假”在短时间内快速、高效解题，当然想要灵活运用这两种解题技巧，还需要我们多多练习，赶快去找题目练起来吧！

行测朴素逻辑：教你一招看破谁在说谎

行测判断推理有类题目出现频次较高且难度较大，那就是真假话问题。真假话问题的考查，如果不能利用命题的矛盾关系以及推理规则解题时，就让很多考生头疼，不知从何下手。此时我们可以利用假设法增加条件后进行推理，但是从哪个条件着手进行假设是快速解题的关键。下面结合一道例题来一窥究竟：

【例题】天使永远说真话，魔鬼永远说假话，人有时说真话有时说假话。现有天使、魔鬼和人各一位，分别穿着红衣服、蓝衣服和白衣服。他们各自叙述如下：

红衣服：”我不是魔鬼。”

蓝衣服：“我不是天使。”

白衣服：“我不是人。”

由此可见：（   ）

A.穿红衣服的是天使           B.穿红衣服的是魔鬼

C.穿红衣服的是人             D.穿白衣服的是魔鬼

【答案】B【解析】根据题干可知“天使说真话”，与天使相关的信息是蓝衣服。假设蓝衣服为天使，则蓝衣服说真话，根据蓝衣服“我不是天使”，可知自相矛盾，所以假设错误，即蓝衣服不是天使，可能是人或魔鬼；又因为魔鬼说假话，所以，蓝衣服如果是魔鬼，不可能说“我不是天使”这种和身份匹配的真话，因此蓝衣服不是魔鬼，只能是人。再根据白衣服说自己不是人，可以确定白衣服说的是真话，白衣服是天使，进一步可以推出红衣服是魔鬼。故答案选B。

回顾这道题目，我们采用的假设法是从提到天使的条件开始假设，为什么要从天使的相关信息开始假设呢？其实是因为天使说真话，涉及真话的条件运用起来更符合我们的思维，不会绕弯子，得出的结论较为确定。如果从提到人的条件开始假设，人是既说真话也说假话，本身情况就比较多，所以从与人相关的信息进行假设不好入手；同样如果从与魔鬼相关的信息去假设，魔鬼是说谎的，那红衣服有可能是天使，有可能是人，还有可能是魔鬼，情况也是不确定的。所以运用假设法关键是要找到情况数相对较少的条件，以此优先假设。

同学们，遇到真假话问题时，如果不能利用矛盾关系和推理规则来解题时，我们可以尝试假设法，从情况数相对较少的条件入手假设，看是否推出矛盾，推出矛盾假设不成立；没有矛盾假设成立。

行测朴素逻辑：看到“可能”就代入，答案藏在选项中

行测考场上时间紧任务重，在更短的时间里做对更多的题目是我们的终极目标。而朴素逻辑可谓是让人欢喜让人忧——选对方法事半功倍，选错方法徒劳无功。所以确定朴素逻辑做题方法就显得格外重要。今天来说一说在朴素逻辑题目中含有“可能”二字的题目。其实“可能”二字意味就着符合题干所给条件的情况不止一种，直接去判断求解很可能是无法得到确切答案的，因此代入排除是一个更为高效且命中率高的方法。我们结合具体的题目来验证一下：

例题：最近上映了一部很受欢迎的电影，小刘购买了4张座位连在一起的电影票，邀请小马、小杨、小廖一同去观看。四人各自随机拿了一张电影票，此时他们分别猜了一下座位情况：

小刘说：“我好像是坐在小马旁边。”

小马说：“我的左手边不是小刘就是小杨。”

小杨说：“我肯定是坐在小廖旁边。”

小廖说：“小刘应该是坐在我的左手边。”

假如他们四人都猜错了，那么他们面向银慕从左到右的正确座位可能是：（   ）

A.小廖、小马、小杨、小刘

B.小刘、小杨、小廖、小马

C.小马、小廖、小杨、小刘

D.小杨、小刘、小廖、小马

【解析】答案：A。问法当中出现“可能”二字，可利用代入排除法解题，验证选项。由小杨猜错了可以排除B、C，由小廖猜错了可以排除D。因此正确答案为A选项。

例题2

针对一块园地，园艺师们提出了如下建议：(1)牡丹、芍药至多种植一种；(2)如果种植芍药，则不能种植蝴蝶兰或者玫瑰；(3)牡丹、玫瑰至少种植一种。实际种植时，上述三条建议只有一条被采纳。

根据以上陈述，以下最可能符合实际种植情况的是：（   ）

A.牡丹、芍药和玫瑰均种

B.种植芍药，但不种蝴蝶兰、玫瑰

C.芍药、蝴蝶兰和玫瑰均种

D.种植蝴蝶兰，但不种植玫瑰、芍药

【答案】A【解析】题干三个条件中不存在对当关系的命题，使用代入法解题。代入A项，则(1)、(2)为假，(3)为真，符合题意；代入B项，则(1)(2)都为真，不符合题意；代入C项，则(1)(3)都为真，不符合题意；代入D项，则(1)(2)都为真，不符合题意。故本题选A。

通过上述两道例题，我们可以发现，看到问法当中出现“可能”二字，就可以尝试根据所给条件进行代入排除，这样难度一下就降低了。希望各位考生在平时的学习中也要善于观察善于总结，用好出题人给我们的提示信息，掌握题目规律，从而做到更快更准。

行测朴素逻辑：假设法的“魔力”，总能给你意外之喜！

朴素逻辑作为行测判断推理的难点，是考生们非常头疼的题型，一方面源于题目本身逻辑性强，难度大；另一方面因为它出题形式比较灵活，没有固定的解题思路。尤其当朴素逻辑题目中的条件“杂”“乱”没有条理，需要同学们用“假设法”解题时，难度往往更大。

假设法是先假设某个条件正确或错误，再依据假设的情况进行推导，若推导的结论与已知条件矛盾，则假设不成立。假设法一般适用于：题干中存在真假话问题且已知条件并无矛盾关系的题目中。一般偏向于从真话进行假设，更容易判断假设的正误。

以下面两道题为例，让同学们感受一下这类题目的特点及假设法的运用：

例题：有四个人，他们分别是小偷、强盗、法官、警察。第一个人说：“第二个人不是小偷。”第二个人说：“第三个是警察。”第三个人说：“第四个人不是法官。”第四个人说：“我不是警察，而且除我之外只有警察会说实话。”

如果第四个人说的是实话，那么以下说法正确的是：（   ）

A.第一个人是警察，第二个人是小偷

B.第一个人是小偷，第四个人是法官

C.第三个人是警察，第四个人是法官

D.第二个人是强盗，第三个人是小偷

【答案】D【解析】题干中四人的话有真有假，且并不存在矛盾关系，考虑使用朴素逻辑中的假设法。根据“第四个人说的是实话”可知，前三个人中，只有警察一个人说实话。因此警察是特殊身份，而其他三个人的话只有第二个人涉及了警察，可以由此进行推理。假设第二个人是警察，那么他说的是真话，则第二个人和第三个人都是警察，有两位警察不符合题干，因此第二个人说假话，所以，第二个人和第三个人都不是警察，那么只能第一个人是警察。因为第三个人不是警察，所以第三个人也说假话，可知第四个人是法官。由第一个人说实话可知第二个人不是小偷，那么第二个人只能是强盗，第三个人是小偷。故本题选D。

例题：警方在一起案件的侦破过程中，抓获了甲、乙、丙三个犯罪嫌疑人。

甲说：“乙在说谎。”

乙说：“丙在说谎。”

丙说：“甲和乙都在说谎。”

由此可推知，三个人中说真话的是：（   ）

A.甲       B.乙      C.丙        D.都没有

【答案】B【解析】采用假设法。相较甲、乙二人，丙的话最特别，因此假设丙说真话，则甲和乙都说谎，而甲说“乙在说谎”，说明甲说的是真话，与前面假设得出的“甲在说谎”矛盾，因此，丙说谎。根据丙说谎，可知乙的表述正确，所以乙说真话。根据乙说真话，可知甲的表述错误，所以甲说谎。故本题选B。

综上，虽然朴素逻辑的题目看着“很难”，但只要用对了方法还是能够顺利解出的，希望各位考生在今后学习中能够针对此类题型多做练习，做题时能够举一反三、灵活运用，从而在考试中能够快速准确得出正确答案！